Primer resumen sobre modelos de clasificación supervisada#
En este capítulo, nos adentraremos en el mundo de los métodos de clasificación supervisada utilizando Python. Comenzaremos nuestra exploración con Random Forest dando continuidad al que ya vimos: Árboles de decisión.
La clasificación supervisada es un pilar fundamental del aprendizaje automático, se centra en construir modelos capaces de predecir etiquetas categóricas basándose en características observadas en los datos. Desde la detección de correos electrónicos no deseados hasta la predicción de enfermedades y la segmentación de clientes, los métodos de clasificación supervisada tienen una amplia gama de aplicaciones en el mundo real.
Después de haber explorado los árboles de decisión, que sirven como bloques constructivos, estamos listos para avanzar hacia modelos más complejos y poderosos. Random Forest, o el “Bosque Aleatorio”, se destaca por su capacidad para operar como un conjunto, o “ensamble”, de árboles de decisión, trabajando juntos para superar las limitaciones de los árboles individuales y proporcionar predicciones más precisas y estables.
A lo largo de este capítulo, no solo cubriremos la teoría y la intuición detrás de Random Forest y otros métodos de clasificación supervisada, sino que también proporcionaremos ejemplos prácticos y ejercicios en Python. Utilizaremos librerías populares como scikit-learn, que ofrece implementaciones eficientes y fáciles de usar de una variedad de algoritmos de aprendizaje automático.
Además de Random Forest, exploraremos otros modelos esenciales en la clasificación supervisada, incluyendo:
Regresión Logística (Logistic Regression): Aunque su nombre pueda sugerirlo, la regresión logística es un método de clasificación ampliamente utilizado. Es especialmente efectivo para casos binarios y se utiliza para estimar probabilidades basadas en una función logística.
Vecinos más Cercanos (K-Nearest Neighbors, K-NN): Este modelo clasifica los nuevos puntos de datos basándose en la “vecindad” de los k puntos más cercanos en el espacio de características. Es un método intuitivo y no paramétrico que se adapta bien a muchas situaciones prácticas.
Máquinas de Vectores de Soporte (Support Vector Machines, SVM): Las SVM son particularmente potentes en espacios de alta dimensión y son adecuadas para casos donde la separación entre clases no es claramente definible. Funcionan construyendo el mejor hiperplano que separa las diferentes clases en el espacio de características.
Gradient Boosting (como XGBoost, LightGBM, CatBoost): Estos algoritmos construyen modelos de predicción de forma secuencial, donde cada nuevo modelo corrige los errores cometidos por los modelos anteriores. Son extremadamente efectivos en competiciones de ciencia de datos y en problemas donde la precisión predictiva es el objetivo principal.
Redes Neuronales Artificiales (Neural Networks): Las redes neuronales son sistemas que imitan la forma en que los humanos aprenden, capaces de modelar relaciones complejas y no lineales. Son particularmente útiles en la clasificación de imágenes, el procesamiento del lenguaje natural, y otras tareas de aprendizaje profundo.
Naive Bayes: Este es un conjunto de algoritmos de clasificación basados en el teorema de Bayes, con la “ingenua” suposición de independencia entre las características. A pesar de su simplicidad, los clasificadores Naive Bayes han funcionado bien en muchas situaciones reales, especialmente en la clasificación de textos.
AdaBoost: AdaBoost, o “Adaptive Boosting”, es un método de ensamble que ajusta los pesos de los clasificadores débiles (tipicamente árboles de decisión de un solo nivel) secuencialmente, enfocándose en los casos más difíciles hasta lograr un clasificador fuerte. Es bien conocido por su eficacia en la mejora de la precisión de cualquier clasificador.
Cada uno de estos modelos tiene sus propias fortalezas y situaciones en las que es más adecuado. A lo largo de este capítulo, exploraremos en detalle cómo cada uno funciona, cómo se implementan en Python utilizando scikit-learn u otras bibliotecas relevantes, y en qué situaciones podrían ser la mejor opción para tus proyectos de clasificación supervisada.
Note
Sintaxis General para Modelos de Clasificación en Scikit-learn
En scikit-learn, la implementación de modelos de clasificación supervisada sigue un patrón consistente, lo que facilita la experimentación con diferentes algoritmos. Este patrón se puede describir en unos pocos pasos generales aplicables a cualquier modelo de clasificación. Aquí te muestro cómo se ve esta sintaxis de manera abstracta:
Pasos Generales
Importar el Modelo: Primero, se importa la clase correspondiente al modelo que deseas utilizar desde scikit-learn.
from sklearn.[modulo] import [Modelo]
Instanciar el Modelo: Creas una instancia del modelo, donde puedes especificar varios hiperparámetros según tus necesidades. Si no estás seguro, puedes empezar con los valores predeterminados.
modelo = [Modelo](hiperparametro1=valor1, hiperparametro2=valor2, ...)
Entrenar el Modelo: Utilizas el método
.fit()para entrenar el modelo con tus datos de entrenamiento. Esto ajustará los parámetros del modelo para minimizar el error de predicción.modelo.fit(X_train, y_train)
Hacer Predicciones: Una vez entrenado el modelo, puedes usar el método
.predict()para hacer predicciones sobre nuevos datos.y_pred = modelo.predict(X_test)
Ejemplo Genérico
Aquí tienes un ejemplo genérico que muestra cómo aplicar estos pasos:
# Paso 1: Importar el modelo
from sklearn.[modulo] import [Modelo]
# Paso 2: Instanciar el modelo con los hiperparámetros deseados
modelo = [Modelo](hiperparametro1=valor1, hiperparametro2=valor2, ...)
# Paso 3: Entrenar el modelo
modelo.fit(X_train, y_train)
# Paso 4: Hacer predicciones
y_pred = modelo.predict(X_test)
Es importante recordar que [modulo], [Modelo], hiperparametro1, valor1, etc., son marcadores de posición. Deben reemplazarce con los nombres específicos y valores relevantes para el modelo que estás utilizando. Esta estructura te permite adaptar fácilmente el código para diferentes modelos de clasificación supervisada en scikit-learn.
Cómo Funciona Random Forest#
Random Forest es un algoritmo de aprendizaje automático basado en ensambles que utiliza múltiples árboles de decisión para realizar sus predicciones. La “magia” de Random Forest radica en la combinación de la simplicidad de los árboles de decisión con la potencia de los modelos de ensamble, lo que resulta en un sistema robusto capaz de manejar tanto tareas de clasificación como de regresión con alta precisión.
Note
La idea central detrás de Random Forest es crear un “bosque” de árboles de decisión donde cada árbol es un poco diferente de los demás. Al hacer una predicción, Random Forest toma las decisiones de todos estos árboles individuales y las combina para producir un resultado más preciso y confiable que el que obtendría un solo árbol de decisión.
Funcionamiento Intuitivo de Random Forest#
Selección de Muestras Aleatorias: Para cada árbol en el bosque, Random Forest selecciona una muestra aleatoria de los datos de entrenamiento. Esto se hace con reemplazo, lo que significa que algunos datos pueden ser seleccionados más de una vez, mientras que otros pueden no ser seleccionados en absoluto.
Construcción de Árboles con Características Aleatorias: Al construir cada árbol, Random Forest no considera todas las características (o variables) disponibles al hacer una división, sino que selecciona un subconjunto aleatorio de características. Esto asegura que los árboles sean diferentes y puedan capturar diversas relaciones en los datos.
Predicción y Votación: Para hacer una predicción, cada árbol en el bosque da su voto. En una tarea de clasificación, la clase más votada es la predicción final del bosque; en una tarea de regresión, el promedio de las predicciones de todos los árboles es el resultado final.
Note
Este proceso de selección aleatoria tanto de muestras como de características, junto con la votación o promediación de las predicciones de los árboles, ayuda a aumentar la precisión y a reducir el sobreajuste, haciendo de Random Forest uno de los algoritmos más poderosos y versátiles en el campo del aprendizaje automático.
Visualización del Algoritmo Random Forest#
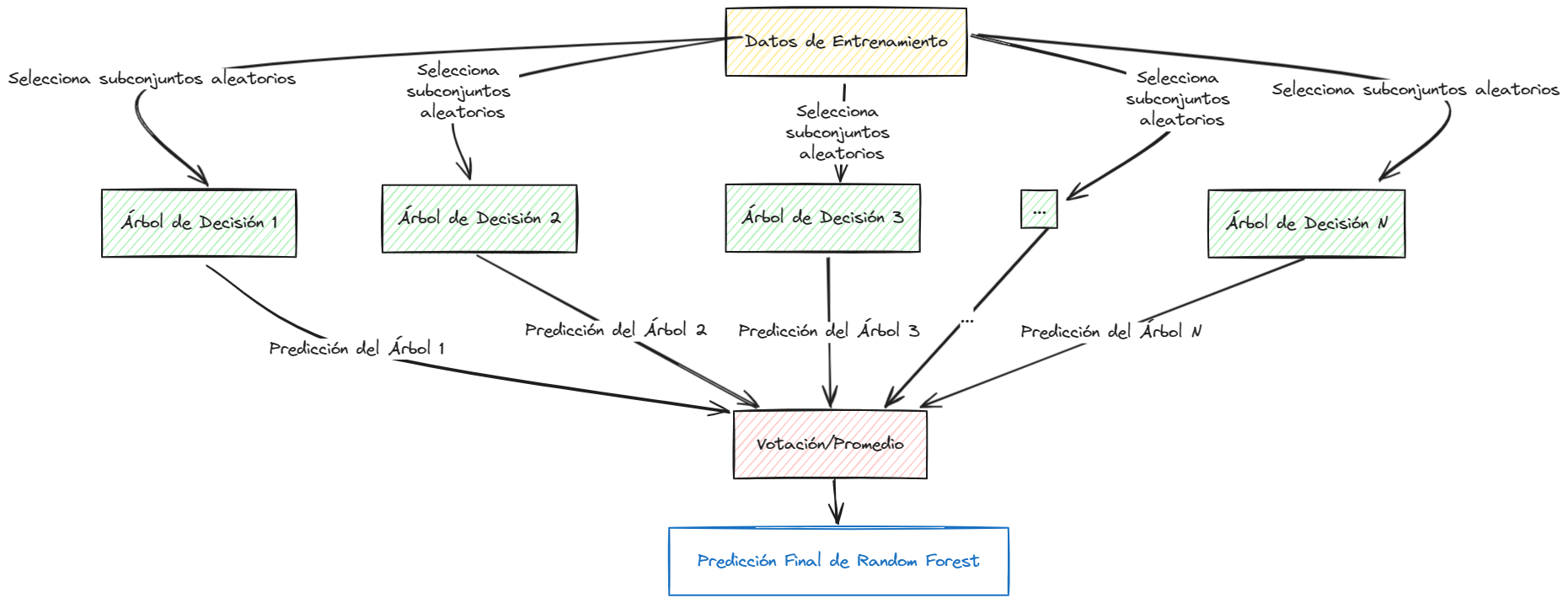
Random Forest es un algoritmo excepcionalmente potente que combina la simplicidad de los árboles de decisión con la robustez de los métodos de ensamble. Su capacidad para manejar grandes conjuntos de datos con alta dimensionalidad, su resistencia al sobreajuste y su facilidad de uso lo convierten en una herramienta valiosa para cualquier científico de datos.
## Ejemplo sencillo
## Dataset de prueba [Iris]
from sklearn import datasets
import pandas as pd
import numpy as np
iris = datasets.load_iris()
iris_df = pd.DataFrame(data= np.c_[iris['data'], iris['target'].astype(int)],
columns= iris['feature_names'] + ['target'])
iris_df.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
iris_df['target'].astype(int).value_counts()
target
0 50
1 50
2 50
Name: count, dtype: int64
## Dividir el dataset en entrenamiento y prueba
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris_df[iris['feature_names']], iris_df['target'], test_size=0.4, stratify=iris_df['target'].astype(int), random_state=0)
print('X train shape:', X_train.shape)
print('X test shape:', X_test.shape)
X train shape: (90, 4)
X test shape: (60, 4)
## Ahora clasificación con Random Forest
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100, random_state=0)
clf.fit(X_train, y_train)
## Predicción
y_pred = clf.predict(X_test)
## Evaluación
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 0.90 0.95 0.93 20
2.0 0.95 0.90 0.92 20
accuracy 0.95 60
macro avg 0.95 0.95 0.95 60
weighted avg 0.95 0.95 0.95 60
Hiperparámetros Importantes de Random Forest#
Random Forest tiene varios hiperparámetros que pueden ajustarse para optimizar su rendimiento en diferentes conjuntos de datos. Algunos de los hiperparámetros más importantes incluyen:
n_estimators: El número de árboles en el bosque. Un mayor número de árboles generalmente mejora el rendimiento, pero también aumenta el tiempo de entrenamiento y la complejidad del modelo.
max_depth: La profundidad máxima de cada árbol. Limitar la profundidad de los árboles puede ayudar a prevenir el sobreajuste.
min_samples_split: El número mínimo de muestras requeridas para dividir un nodo interno. Aumentar este valor puede ayudar a prevenir el sobreajuste.
min_samples_leaf: El número mínimo de muestras requeridas para ser una hoja. Al igual que
min_samples_split, aumentar este valor puede ayudar a prevenir el sobreajuste.max_features: El número de características a considerar al buscar la mejor división. Reducir este valor puede acelerar el entrenamiento y ayudar a prevenir el sobreajuste.
bootstrap: Indica si se deben usar muestras de arranque al construir árboles. Si es
True, se utiliza el muestreo con reemplazo.random_state: Controla la aleatoriedad del estimador. Establecer un valor fijo para
random_stategarantiza que los resultados sean reproducibles.
Estos hiperparámetros y otros permiten ajustar la complejidad y el rendimiento de Random Forest para adaptarse a las necesidades específicas de tu problema de clasificación. Experimentar con diferentes valores y técnicas de validación cruzada te ayudará a encontrar la configuración óptima para tu conjunto de datos.
Como funciona la Regresión Logística#
A pesar de su nombre, la regresión logística es un método de clasificación ampliamente utilizado en el aprendizaje automático. Es especialmente efectivo para problemas de clasificación binaria, donde el objetivo es predecir una de dos clases posibles, como “sí” o “no”, “spam” o “no spam”, “enfermo” o “sano”, etc.
Note
La regresión logística se basa en el concepto de regresión lineal, pero en lugar de predecir valores continuos, estima la probabilidad de que un punto de datos pertenezca a una clase en particular. Utiliza una función logística para transformar la salida de un modelo lineal en una probabilidad entre 0 y 1.
Funcionamiento Intuitivo de la Regresión Logística#
Modelo Lineal: La regresión logística comienza con un modelo lineal que combina las características de entrada ponderadas por coeficientes. La salida de este modelo lineal se pasa a través de una función logística, que transforma los valores en el rango de 0 a 1.
Función Logística: La función logística, también conocida como función sigmoide, se define como:
Donde \(z\) es la salida del modelo lineal. La función logística mapea cualquier valor real a un valor en el rango de 0 a 1, lo que se interpreta como la probabilidad de que un punto de datos pertenezca a la clase positiva.
Umbral de Decisión: Para hacer predicciones, la regresión logística compara la probabilidad estimada con un umbral (generalmente 0.5). Si la probabilidad es mayor que el umbral, el punto de datos se clasifica como positivo; de lo contrario, se clasifica como negativo.
Note
La regresión logística es un modelo lineal simple pero efectivo que se utiliza en una amplia variedad de aplicaciones de clasificación. Es fácil de interpretar, computacionalmente eficiente y se puede extender para manejar problemas de clasificación multiclase y no lineales.
Visualización del Algoritmo de Regresión Logística#
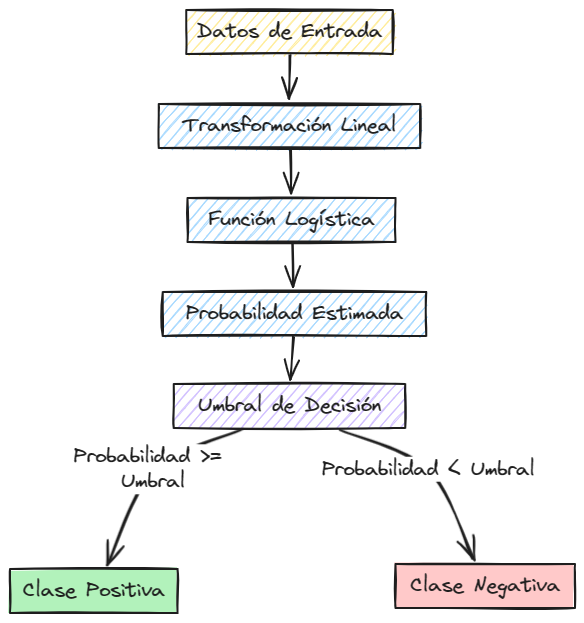
La regresión logística es un modelo lineal simple pero poderoso que se utiliza en una amplia variedad de aplicaciones de clasificación. Su capacidad para estimar probabilidades y su facilidad de interpretación lo convierten en una herramienta valiosa para cualquier científico de datos.
## Regresón Logistica
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0)
clf.fit(X_train, y_train)
## Predicción
y_pred = clf.predict(X_test)
## Evaluación
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 1.00 0.95 0.97 20
2.0 0.95 1.00 0.98 20
accuracy 0.98 60
macro avg 0.98 0.98 0.98 60
weighted avg 0.98 0.98 0.98 60
Como funciona K-Nearest Neighbors (K-NN)#
K-Nearest Neighbors (K-NN) es un algoritmo de clasificación simple y no paramétrico que se basa en la idea de que los puntos de datos similares tienden a pertenecer a la misma clase. En lugar de aprender explícitamente un modelo, K-NN clasifica los puntos de datos basándose en la similitud con los puntos de datos de entrenamiento más cercanos.
Note
La “vecindad” en K-NN se define por una métrica de distancia, como la distancia euclidiana o la distancia de Manhattan. El hiperparámetro k especifica el número de vecinos más cercanos que se consideran al hacer una predicción.
Funcionamiento Intuitivo de K-NN#
Almacenamiento de Datos de Entrenamiento: K-NN almacena los datos de entrenamiento en memoria y no aprende explícitamente un modelo. Para hacer una predicción, calcula la distancia entre el punto de datos de entrada y todos los puntos de datos de entrenamiento.
Selección de Vecinos: K-NN identifica los
kpuntos de datos de entrenamiento más cercanos al punto de datos de entrada. La elección dekes un hiperparámetro crítico que afecta el rendimiento del algoritmo.Votación de Vecinos: Para hacer una predicción, K-NN asigna la clase más común entre los
kvecinos más cercanos al punto de datos de entrada. En una tarea de regresión, K-NN puede predecir el valor medio de loskvecinos más cercanos.
Note
K-NN es un algoritmo simple y fácil de entender que se puede utilizar para una variedad de problemas de clasificación y regresión. Sin embargo, su rendimiento puede verse afectado por la elección de k y la escala de las características, y puede ser computacionalmente costoso en conjuntos de datos grandes.
Visualización del Algoritmo K-NN#
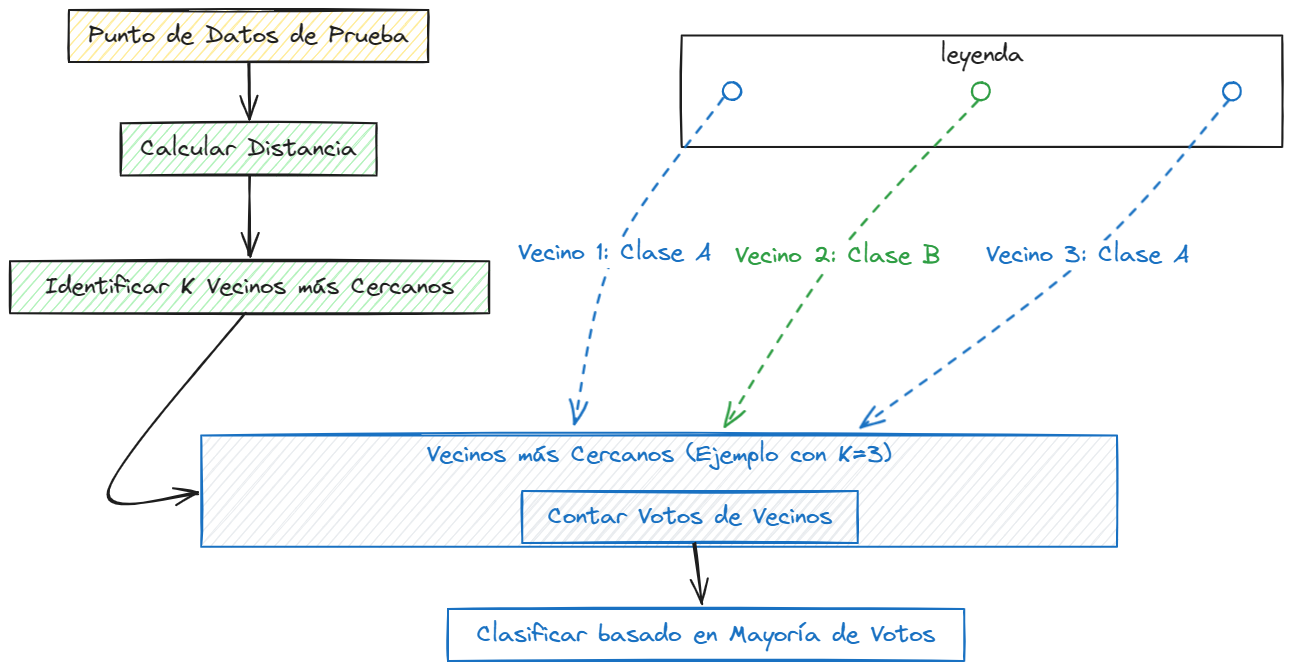
K-NN es un algoritmo intuitivo y fácil de entender que se basa en la idea de que los puntos de datos similares tienden a pertenecer a la misma clase. Aunque es simple, K-NN puede ser efectivo en una variedad de situaciones y es un buen punto de partida para problemas de clasificación.
## KNN
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)
## Predicción
y_pred = clf.predict(X_test)
## Evaluación
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 1.00 1.00 1.00 20
2.0 1.00 1.00 1.00 20
accuracy 1.00 60
macro avg 1.00 1.00 1.00 60
weighted avg 1.00 1.00 1.00 60
Hiperparámetros Importantes de K-NN#
K-NN tiene varios hiperparámetros que pueden ajustarse para optimizar su rendimiento en diferentes conjuntos de datos. Algunos de los hiperparámetros más importantes incluyen:
n_neighbors: El número de vecinos más cercanos que se consideran al hacer una predicción. Un valor más alto de
n_neighborssuaviza la frontera de decisión, mientras que un valor más bajo puede llevar a un sobreajuste.weights: La función de peso utilizada en la predicción. Las opciones comunes incluyen
uniform, donde todos los vecinos tienen el mismo peso, ydistance, donde los vecinos más cercanos tienen más peso.metric: La métrica de distancia utilizada para calcular la similitud entre puntos de datos. Las opciones comunes incluyen la distancia euclidiana, la distancia de Manhattan y la distancia de Minkowski.
algorithm: El algoritmo utilizado para calcular los vecinos más cercanos. Las opciones comunes incluyen
brute, que calcula todas las distancias, ykd_treeyball_tree, que utilizan estructuras de datos especiales para acelerar el cálculo.leaf_size: El tamaño de la hoja pasado a los algoritmos
kd_treeyball_tree. Un valor más bajo puede acelerar el cálculo, pero también puede aumentar el uso de memoria.p: El parámetro de potencia para la métrica de Minkowski. Cuando
p = 1, esto equivale a la distancia de Manhattan; cuandop = 2, esto equivale a la distancia euclidiana.
Estos hiperparámetros y otros permiten ajustar la complejidad y el rendimiento de K-NN para adaptarse a las necesidades específicas de tu problema de clasificación. Experimentar con diferentes valores y técnicas de validación cruzada te ayudará a encontrar la configuración óptima para tu conjunto de datos.
Conclusiones#
En este capítulo, exploramos varios modelos de clasificación supervisada esenciales en el aprendizaje automático, incluyendo Random Forest, Regresión Logística y K-Nearest Neighbors (K-NN). Cada uno de estos modelos tiene sus propias fortalezas y debilidades, y es adecuado para diferentes tipos de problemas de clasificación.
Los demás modelos de clasificación supervisada que exploraremos en los siguientes capítulos, como Máquinas de Vectores de Soporte (SVM), Gradient Boosting, Redes Neuronales Artificiales y Naive Bayes, ampliarán aún más nuestro repertorio de herramientas de aprendizaje automático. Al comprender cómo funcionan estos modelos y cuándo es apropiado utilizarlos.