Segundo resumen sobre modelos de clasificación supervisada#
En este capítulo, revisaremos los modelos de clasificación que no se vieron en el primer resumen. Veremos los siguientes modelos:
Support Vector Machines (SVM)
Naive Bayes
Gradient Boosting
Redes Neuronales Artificiales
Como en el anterior capítulo, no solo cubriremos la teoría y la intuición detrás de Random Forest y otros métodos de clasificación supervisada, sino que también proporcionaremos ejemplos prácticos y ejercicios en Python. Utilizaremos librerías populares como scikit-learn, que ofrece implementaciones eficientes y fáciles de usar de una variedad de algoritmos de aprendizaje automático.
Cada uno de estos modelos tiene sus propias fortalezas y situaciones en las que es más adecuado. A lo largo de este capítulo, exploraremos en detalle cómo cada uno funciona, cómo se implementan en Python utilizando scikit-learn u otras bibliotecas relevantes, y en qué situaciones podrían ser la mejor opción para tus proyectos de clasificación supervisada.
Recordemos la estructura abstracta para entrenar modelos en scikit-learn:
Note
Sintaxis General para Modelos de Clasificación en Scikit-learn
En scikit-learn, la implementación de modelos de clasificación supervisada sigue un patrón consistente, lo que facilita la experimentación con diferentes algoritmos. Este patrón se puede describir en unos pocos pasos generales aplicables a cualquier modelo de clasificación. Aquí te muestro cómo se ve esta sintaxis de manera abstracta:
Pasos Generales
Importar el Modelo: Primero, se importa la clase correspondiente al modelo que deseas utilizar desde scikit-learn.
from sklearn.[modulo] import [Modelo]
Instanciar el Modelo: Creas una instancia del modelo, donde puedes especificar varios hiperparámetros según tus necesidades. Si no estás seguro, puedes empezar con los valores predeterminados.
modelo = [Modelo](hiperparametro1=valor1, hiperparametro2=valor2, ...)
Entrenar el Modelo: Utilizas el método
.fit()para entrenar el modelo con tus datos de entrenamiento. Esto ajustará los parámetros del modelo para minimizar el error de predicción.modelo.fit(X_train, y_train)
Hacer Predicciones: Una vez entrenado el modelo, puedes usar el método
.predict()para hacer predicciones sobre nuevos datos.y_pred = modelo.predict(X_test)
Ejemplo Genérico
Aquí tienes un ejemplo genérico que muestra cómo aplicar estos pasos:
# Paso 1: Importar el modelo
from sklearn.[modulo] import [Modelo]
# Paso 2: Instanciar el modelo con los hiperparámetros deseados
modelo = [Modelo](hiperparametro1=valor1, hiperparametro2=valor2, ...)
# Paso 3: Entrenar el modelo
modelo.fit(X_train, y_train)
# Paso 4: Hacer predicciones
y_pred = modelo.predict(X_test)
Es importante recordar que [modulo], [Modelo], hiperparametro1, valor1, etc., son marcadores de posición. Deben reemplazarce con los nombres específicos y valores relevantes para el modelo que estás utilizando. Esta estructura te permite adaptar fácilmente el código para diferentes modelos de clasificación supervisada en scikit-learn.
Cómo Funciona Support Vector Machines (SVM)#
Support Vector Machines (SVM) representa uno de los algoritmos más robustos y precisos dentro del aprendizaje supervisado, especialmente utilizado para problemas de clasificación. Este algoritmo se basa en la idea de encontrar el mejor hiperplano que separa las distintas clases en el espacio de características.
Note
El hiperplano en el contexto de SVM es conceptualmente similar a una línea de división en 2D, pero extendido a espacios de mayor dimensión. Su objetivo es maximizar el margen entre las clases de datos, siendo este margen la distancia mínima entre el hiperplano y los puntos más cercanos de las clases (vectores de soporte).
Principios Fundamentales de SVM#
Identificación del Mejor Hiperplano: SVM comienza el proceso de clasificación buscando el hiperplano que ofrece la mayor separación (margen) entre las diferentes clases. En un espacio de dos dimensiones, este hiperplano puede visualizarse como una línea.
Maximización del Margen: El margen se define como la distancia entre el hiperplano y los vectores de soporte más cercanos. Los vectores de soporte son aquellos puntos de datos que están más cerca del hiperplano. SVM optimiza este margen para mejorar la capacidad del modelo para generalizar bien a nuevos datos.
Uso del Truco del Kernel: En situaciones donde los datos no son linealmente separables, SVM utiliza técnicas de kernel para transformar el espacio de entrada en un espacio de mayor dimensión donde los datos pueden ser separados linealmente. Esto permite a SVM manejar eficazmente relaciones complejas y no lineales entre las características.
Note
A través del truco del kernel, SVM es capaz de realizar clasificaciones complejas y no lineales utilizando espacios de características transformados, sin necesidad de calcular explícitamente las dimensiones adicionales.
Visualización del Algoritmo SVM#
Imagina que estás en un campo abierto donde se encuentran dispersos dos tipos de flores. Tu tarea es trazar una línea recta (en este caso, el hiperplano) que separe lo mejor posible estos dos tipos de flores. El enfoque de SVM no solo se centra en trazar esta línea sino en posicionarla de tal manera que la distancia (margen) entre la línea y las flores más cercanas a ella (de ambos tipos) sea la máxima posible. Esto es equivalente a maximizar la tolerancia al error en la clasificación de futuras muestras de flores.
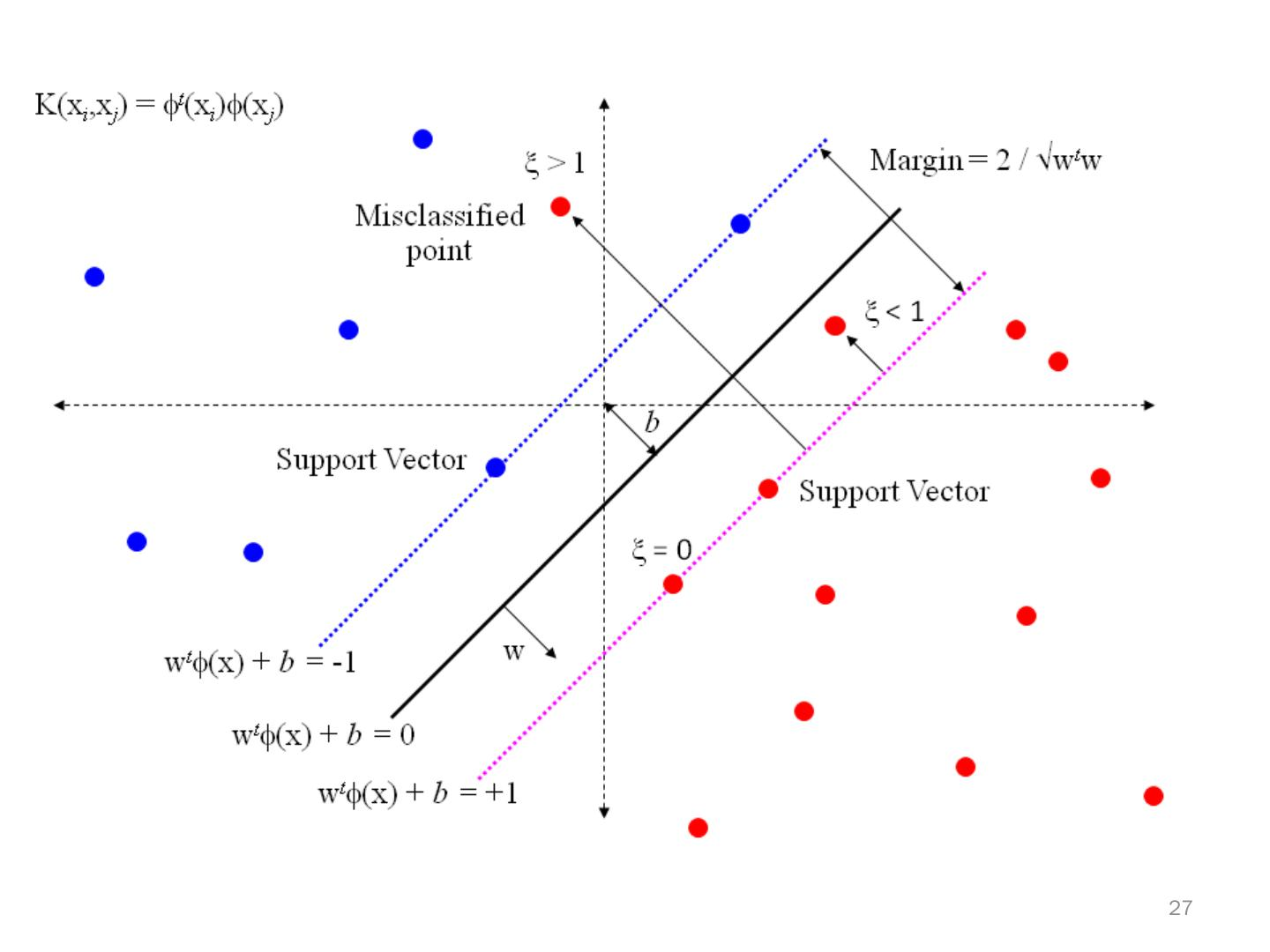
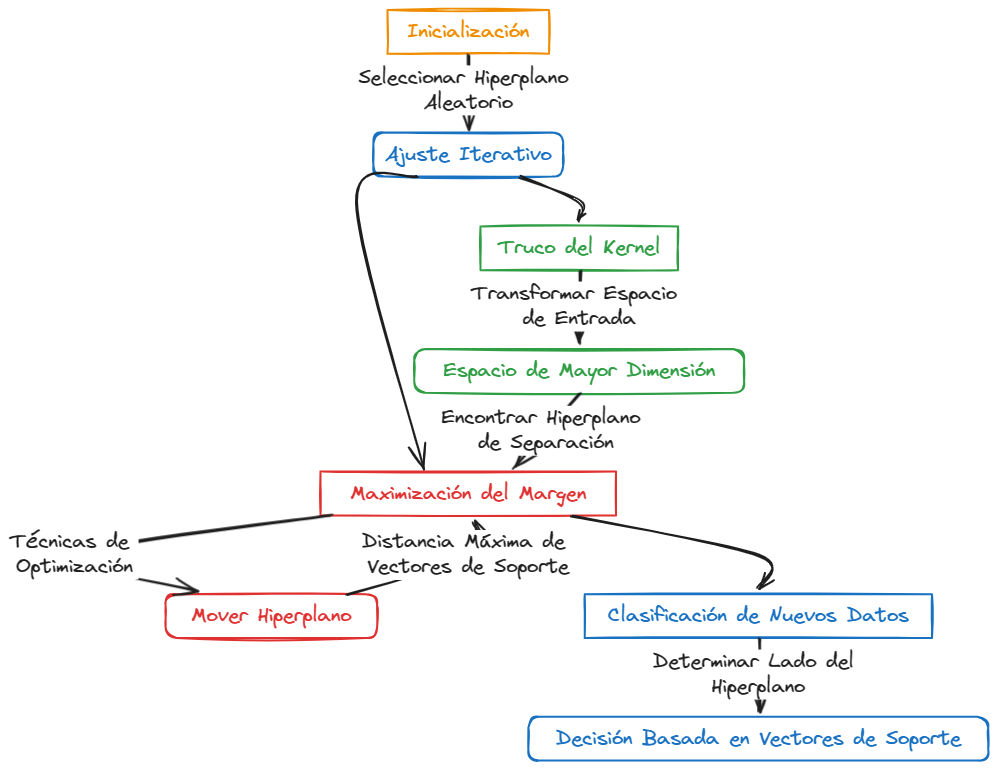
SVM se destaca por su efectividad en espacios de alta dimensión y su capacidad para manejar fronteras de decisión complejas y no lineales, gracias al uso de funciones kernel. Este enfoque, centrado en la maximización del margen y en la importancia crítica de los vectores de soporte, permite que SVM sea altamente efectivo y preciso en la clasificación, incluso en situaciones donde la relación entre las características no es inmediatamente evidente.
## Importamos warnings para evitar los mensajes de advertencia
import warnings
warnings.filterwarnings('ignore')
## Ejemplo sencillo
## Dataset de prueba [Iris]
from sklearn import datasets
import pandas as pd
import numpy as np
iris = datasets.load_iris()
iris_df = pd.DataFrame(data= np.c_[iris['data'], iris['target'].astype(int)],
columns= iris['feature_names'] + ['target'])
iris_df.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0.0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0.0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0.0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0.0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0.0 |
iris_df['target'].astype(int).value_counts()
target
0 50
1 50
2 50
Name: count, dtype: int64
## Dividir el dataset en entrenamiento y prueba
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris_df[iris['feature_names']], iris_df['target'], test_size=0.4, stratify=iris_df['target'].astype(int), random_state=0)
print('X train shape:', X_train.shape)
print('X test shape:', X_test.shape)
X train shape: (90, 4)
X test shape: (60, 4)
## Ahora clasificación con SVM
from sklearn.svm import SVC
clf = SVC(kernel='linear', C=1.0, random_state=0)
clf.fit(X_train, y_train)
## Predicción
y_pred = clf.predict(X_test)
## Evaluación
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 1.00 1.00 1.00 20
2.0 1.00 1.00 1.00 20
accuracy 1.00 60
macro avg 1.00 1.00 1.00 60
weighted avg 1.00 1.00 1.00 60
Hipérparámetros Importantes de SVM#
SVM tiene varios hiperparámetros que pueden ajustarse para mejorar el rendimiento del modelo. scikit-learn proporciona valores predeterminados razonables para estos hiperparámetros, pero es importante comprender cómo afectan al modelo. Algunos de los hiperparámetros más importantes de SVM son:
c: Parámetro de regularización que controla la compensación entre la maximización del margen y la minimización de la clasificación incorrecta. Un valor más alto de
Cdará como resultado un margen más estrecho pero una clasificación más precisa.kernel: Especifica el tipo de kernel a utilizar en la transformación de los datos. Los kernels comunes incluyen
linear,poly,rbf(radial basis function), ysigmoid.gamma: Coeficiente del kernel para los kernels
rbf,poly, ysigmoid. Un valor más alto degammadará como resultado un ajuste más preciso a los datos de entrenamiento, pero puede llevar a un sobreajuste.
Cómo Funciona Naive Bayes#
Naive Bayes es un clasificador probabilístico que se basa en el teorema de Bayes, junto con una suposición simplificadora pero poderosa: la independencia condicional entre cada par de características dada la variable de clase. Este clasificador es ampliamente utilizado en tareas de clasificación debido a su simplicidad, eficiencia y efectividad, especialmente en el procesamiento de texto y filtrado de spam.
Note
El corazón de Naive Bayes es el teorema de Bayes, que permite calcular la probabilidad posterior de una clase, dadas ciertas características observadas, utilizando la probabilidad previa de la clase y las probabilidades de esas características dada la clase.
Fundamentos Detallados de Naive Bayes#
Teorema de Bayes: Este teorema es esencial para entender cómo Naive Bayes actualiza las probabilidades de las hipótesis a medida que se dispone de nueva evidencia. Matemáticamente, el teorema se expresa como (P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}), donde (P(A|B)) es la probabilidad de (A) dado (B).
Independencia de las Características: A pesar de que en la realidad las características pueden estar relacionadas, Naive Bayes simplifica los cálculos asumiendo que son independientes entre sí dada la clase. Esta suposición naive permite que el modelo se entrene y ejecute eficientemente incluso en conjuntos de datos de alta dimensión.
Cálculo de Probabilidades: Naive Bayes calcula la probabilidad de cada clase dadas las características observadas y selecciona la clase con la mayor probabilidad como la predicción. Este proceso implica multiplicar las probabilidades de las características observadas, ajustadas por las probabilidades previas de las clases.
Note
Aunque la suposición de independencia puede parecer una gran simplificación, Naive Bayes funciona sorprendentemente bien en muchos escenarios reales. Esto se debe a que, para la tarea de clasificación, lo que importa es la probabilidad relativa de las clases, no el valor exacto de las probabilidades.
Aplicaciones Extendidas de Naive Bayes#
Clasificación de Textos y Filtrado de Spam: Distinguir entre correos electrónicos legítimos y no deseados basándose en la presencia de ciertas palabras clave.
Diagnóstico Médico: Predecir la presencia de enfermedades a partir de síntomas y resultados de pruebas, tratando cada síntoma o resultado de prueba como una característica independiente.
Detección de Sentimientos en Textos: Determinar si una opinión expresada en texto es positiva, negativa o neutral, analizando las palabras y frases utilizadas.
Ejemplo Intuitivo y Visual#
Considera el problema de clasificar animales en “gatos” y “perros” basado en características como “tamaño” y “sonido”. Naive Bayes miraría cada característica individualmente, calculando cómo afecta la probabilidad de que el animal sea un gato o un perro, sin preocuparse por las correlaciones entre “tamaño” y “sonido”. Si históricamente los animales pequeños que maúllan son más a menudo gatos, Naive Bayes inclinará fuertemente su predicción hacia “gato” cuando se encuentre con un animal pequeño que maúlla, independientemente de otras correlaciones.
Naive Bayes demuestra que incluso bajo suposiciones simplificadoras, se pueden desarrollar modelos poderosos y eficientes para clasificación. Su rendimiento, especialmente en tareas de clasificación de texto y situaciones con conjuntos de datos de alta dimensión, subraya la importancia de las técnicas probabilísticas en el aprendizaje automático y la ciencia de datos.
# Ejemplo de Implementación con Naive Bayes en scikit-learn
from sklearn.naive_bayes import GaussianNB
# Crear y entrenar el modelo Naive Bayes
gnb = GaussianNB()
gnb.fit(X_train, y_train)
# Realizar predicciones y evaluar el modelo
y_pred = gnb.predict(X_test)
# Evaluación
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 0.95 0.95 0.95 20
2.0 0.95 0.95 0.95 20
accuracy 0.97 60
macro avg 0.97 0.97 0.97 60
weighted avg 0.97 0.97 0.97 60
Hiperparámetros de Naive Bayes#
Aunque Naive Bayes es un modelo relativamente simple, tiene algunos hiperparámetros que pueden ajustarse para mejorar su rendimiento. Algunos de los hiperparámetros más comunes son:
alpha: Parámetro de suavizado de Laplace, que evita la probabilidad cero para características no observadas en el conjunto de entrenamiento. Un valor más alto de
alphasuaviza las estimaciones de probabilidad, lo que puede ser útil para evitar el sobreajuste.fit_prior: Indica si se deben aprender las probabilidades previas de las clases a partir de los datos de entrenamiento. Si se establece en
False, se utilizarán probabilidades previas uniformes.class_prior: Proporciona probabilidades previas específicas de las clases. Si no se especifica, se utilizarán probabilidades previas uniformes.
Cómo Funciona Gradient Boosting#
Gradient Boosting es una técnica de aprendizaje automático que construye un modelo predictivo en forma de un conjunto de modelos de predicción débiles, generalmente árboles de decisión. A diferencia de Random Forest, que entrena cada árbol de forma independiente, Gradient Boosting entrena cada árbol de forma secuencial, mejorando los errores de los árboles anteriores.
Note
El término “Gradient Boosting” se refiere a la técnica de optimización utilizada para minimizar la función de pérdida del modelo, ajustando los parámetros del modelo en la dirección que reduce el gradiente de la función de pérdida.
Principios Fundamentales de Gradient Boosting#
Modelos de Predicción Débiles: En Gradient Boosting, los modelos de predicción débiles, como árboles de decisión poco profundos, se combinan para formar un modelo más fuerte. Cada árbol se enfoca en corregir los errores de los árboles anteriores, en lugar de predecir directamente la variable objetivo.
Optimización Secuencial: A diferencia de Random Forest, donde los árboles se entrenan de forma independiente, en Gradient Boosting, los árboles se entrenan secuencialmente. Cada árbol se ajusta para minimizar la función de pérdida del modelo, que mide la diferencia entre las predicciones del modelo y los valores reales.
Uso de Gradientes: El algoritmo de Gradient Boosting utiliza gradientes de la función de pérdida para ajustar los parámetros del modelo en la dirección que minimiza la pérdida. Este enfoque de optimización basado en gradientes permite que el modelo mejore gradualmente a medida que se agregan más árboles.
Visualización del Algoritmo Gradient Boosting#
Imagina que estás subiendo una colina y quieres llegar a la cima lo más rápido posible. En lugar de elegir la ruta más corta de antemano, decides dar pequeños pasos en la dirección que te lleva más alto en cada paso. Este enfoque te permite avanzar gradualmente hacia la cima, incluso si no puedes ver la cima desde tu posición actual.

Gradient Boosting sigue un enfoque similar, mejorando el modelo de forma incremental en lugar de intentar ajustar todos los parámetros de una vez. Cada árbol de decisión se enfoca en corregir los errores de los árboles anteriores, lo que resulta en un modelo final que es una combinación ponderada de todos los árboles.
Aplicaciones y Ventajas de Gradient Boosting#
Clasificación y Regresión: Gradient Boosting es efectivo tanto para problemas de clasificación como de regresión, y es especialmente útil cuando se requiere un alto nivel de precisión.
Manejo de Datos Desbalanceados: Debido a su capacidad para ajustar los errores de los modelos anteriores, Gradient Boosting puede manejar eficazmente conjuntos de datos desbalanceados.
Interpretación de Características: Aunque Gradient Boosting es un modelo complejo, se pueden utilizar técnicas como la importancia de las características para comprender qué características son más influyentes en las predicciones.
## Implementación de gradient boosting
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=0)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 1.00 1.00 1.00 20
1.0 0.95 0.95 0.95 20
2.0 0.95 0.95 0.95 20
accuracy 0.97 60
macro avg 0.97 0.97 0.97 60
weighted avg 0.97 0.97 0.97 60
Hiperparámetros Importantes de Gradient Boosting#
Gradient Boosting tiene varios hiperparámetros que pueden ajustarse para mejorar el rendimiento del modelo. Algunos de los hiperparámetros más importantes son:
n_estimators: Número de árboles de decisión que se utilizarán en el modelo. Un valor más alto de
n_estimatorspuede mejorar la precisión del modelo, pero también aumenta el riesgo de sobreajuste.learning_rate: Tasa de aprendizaje que controla la contribución de cada árbol al modelo. Un valor más bajo de
learning_raterequerirá más árboles para alcanzar la misma precisión, pero puede mejorar la generalización.max_depth: Profundidad máxima de cada árbol de decisión. Un valor más alto de
max_depthpermitirá que los árboles sean más complejos, lo que puede llevar a un sobreajuste.subsample: Proporción de muestras utilizadas para entrenar cada árbol. Un valor más bajo de
subsamplepuede reducir el riesgo de sobreajuste, pero también puede disminuir la precisión del modelo.
Cómo Funcionan las Redes Neuronales Artificiales#
Las Redes Neuronales Artificiales (ANN) son un modelo de aprendizaje profundo inspirado en la estructura y el funcionamiento del cerebro humano. Estas redes están compuestas por capas de neuronas artificiales que se organizan en una arquitectura de red, con conexiones entre las neuronas que transmiten señales y aprenden a partir de los datos.
Note
El término “profundo” en el aprendizaje profundo se refiere a la presencia de múltiples capas ocultas en la red neuronal, lo que permite que el modelo aprenda representaciones jerárquicas de los datos.
Principios Fundamentales de las Redes Neuronales#
Neuronas Artificiales: Las neuronas artificiales son unidades computacionales que reciben entradas, aplican una transformación no lineal a esas entradas y generan una salida. Cada neurona está conectada a otras neuronas a través de conexiones ponderadas.
Capas de Neuronas: Las neuronas en una red neuronal se organizan en capas, que incluyen una capa de entrada, una o más capas ocultas y una capa de salida. Las capas ocultas permiten que la red aprenda representaciones complejas de los datos.
Conexiones Ponderadas: Las conexiones entre las neuronas tienen pesos asociados que se ajustan durante el proceso de entrenamiento. Estos pesos determinan la importancia de las entradas para la salida de la neurona.
Entrenamiento de Redes Neuronales#
El entrenamiento de una red neuronal implica dos fases clave: propagación hacia adelante (forward propagation) y retropropagación (backpropagation). Durante la propagación hacia adelante, las entradas se pasan a través de la red, y las salidas se calculan utilizando los pesos actuales. Durante la retropropagación, se calculan los gradientes de la función de pérdida con respecto a los pesos de la red, y estos gradientes se utilizan para ajustar los pesos a través de un proceso de optimización.
Note
El proceso de retropropagación es fundamental para el entrenamiento de redes neuronales, ya que permite que la red ajuste los pesos de manera que minimice la función de pérdida, mejorando así la precisión del modelo.
Aplicaciones y Ventajas de las Redes Neuronales#
Visión por Computadora: Las redes neuronales convolucionales (CNN) son ampliamente utilizadas en tareas de visión por computadora, como la clasificación de imágenes y la detección de objetos.
Procesamiento del Lenguaje Natural: Las redes neuronales recurrentes (RNN) y las redes neuronales transformadoras (Transformer) son efectivas en tareas de procesamiento del lenguaje natural, como la traducción automática y la generación de texto.
Reconocimiento de Voz: Las redes neuronales son fundamentales en sistemas de reconocimiento de voz, como los asistentes virtuales y los sistemas de transcripción de voz a texto.
Aprendizaje Profundo: Las redes neuronales son la base del aprendizaje profundo, un subcampo del aprendizaje automático que se centra en modelos de múltiples capas para aprender representaciones jerárquicas de los datos.
## Entrenamiento de una red neuronal
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5, 2), random_state=1)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 0.00 0.00 0.00 20
1.0 0.00 0.00 0.00 20
2.0 0.33 1.00 0.50 20
accuracy 0.33 60
macro avg 0.11 0.33 0.17 60
weighted avg 0.11 0.33 0.17 60
Conclusiones#
En este capítulo, exploramos varios modelos de clasificación supervisada, incluidos Support Vector Machines (SVM), Naive Bayes, Gradient Boosting y Redes Neuronales Artificiales. Cada uno de estos modelos tiene sus propias fortalezas y aplicaciones, y es importante comprender cómo funcionan y cuándo es apropiado utilizarlos.