Regresión Lineal Simple: Teoría y Práctica#
# Importamos las bibliotecas necesarias
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# Configuración básica de matplotlib
plt.rcParams['figure.dpi'] = 100
plt.rcParams['figure.figsize'] = [10, 6]
1. El Modelo Matemático#
Fundamentos
La regresión lineal simple es un método estadístico que modeliza la relación entre una variable dependiente (y) y una variable independiente (x). Es “simple” porque solo hay una variable independiente y “lineal” porque el modelo es lineal en los parámetros.
1.1 Definición Formal#
El modelo se expresa como:
donde:
\(y_i\) es la variable dependiente (respuesta)
\(x_i\) es la variable independiente (predictora)
\(\beta_0\) es el intercepto
\(\beta_1\) es la pendiente
\(\epsilon_i\) es el término de error aleatorio
1.2 Supuestos del Modelo#
Los supuestos fundamentales son:
Supuesto |
Expresión Matemática |
Interpretación |
|---|---|---|
1 |
\(E(\epsilon_i) = 0\) |
El modelo es correcto y \(E(y_i) = \beta_0 + \beta_1 x_i\) |
2 |
\(var(\epsilon_i) = \sigma^2\) |
Homocedasticidad (varianza constante) |
3 |
\(cov(\epsilon_i, \epsilon_j) = 0\) |
Errores no correlacionados |
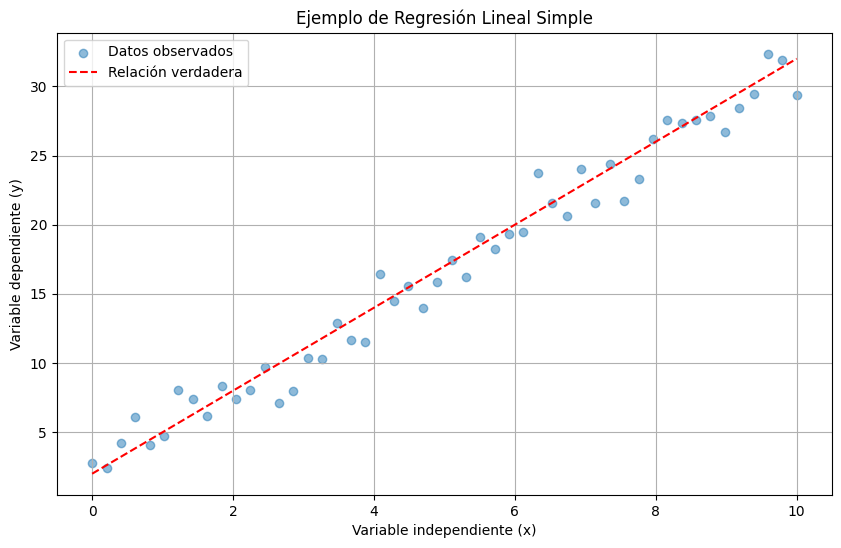
Veamos un ejemplo con datos simulados:
# Generamos datos que cumplen los supuestos
np.random.seed(42)
n = 50
x = np.linspace(0, 10, n)
epsilon = np.random.normal(0, 1.5, n) # Errores normales independientes
beta0_true, beta1_true = 2, 3
y = beta0_true + beta1_true * x + epsilon
# Visualización
plt.scatter(x, y, alpha=0.5, label='Datos observados')
plt.plot(x, beta0_true + beta1_true * x, 'r--', label='Relación verdadera')
plt.xlabel('Variable independiente (x)')
plt.ylabel('Variable dependiente (y)')
plt.title('Ejemplo de Regresión Lineal Simple')
plt.legend()
plt.grid(True)
plt.show()
2. Estimación de Parámetros#
2.1 Método de Mínimos Cuadrados#
Principio de Mínimos Cuadrados
El método busca los valores de \(\beta_0\) y \(\beta_1\) que minimizan la suma de cuadrados de los residuos:
\(\sum_{i=1}^n (y_i - \hat{y}i)^2 = \sum{i=1}^n (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2\)
Objetivo
Encontrar los valores de \(\beta_0\) y \(\beta_1\) que minimicen la suma de los cuadrados de las diferencias entre los valores observados y los valores predichos.
Definimos la función objetivo:
2.2 Condiciones de Primer Orden#
Para minimizar \(S(\beta_0, \beta_1)\), necesitamos que:
2.2.1 Primera Derivada Parcial#
Desarrollamos \(\frac{\partial S}{\partial \beta_0}\):
2.2.2 Segunda Derivada Parcial#
Desarrollamos \(\frac{\partial S}{\partial \beta_1}\):
2.3 Sistema de Ecuaciones Normales#
De (4):
De (5):
2.4 Solución del Sistema#
2.4.1 Obtención de \(\beta_0\)#
De (6):
2.4.2 Obtención de \(\beta_1\)#
Reordenando términos:
2.4.3 Forma Alternativa de \(\beta_1\)#
Podemos reescribir \(\beta_1\) en términos de desviaciones respecto a la media:
2.5 Verificación de Mínimo#
Para confirmar que hemos encontrado un mínimo y no un máximo, verificamos las segundas derivadas:
La matriz Hessiana es:
Es definida positiva, confirmando que hemos encontrado un mínimo global.
2.6 Propiedades Algebraicas#
Las soluciones tienen las siguientes propiedades:
\(\sum_{i=1}^n (y_i - \hat{y}_i) = 0\)
\(\sum_{i=1}^n x_i(y_i - \hat{y}_i) = 0\)
\(\sum_{i=1}^n \hat{y}_i = \sum_{i=1}^n y_i\)
\(\hat{y} = \bar{y}\)
Note
Estas propiedades son consecuencia directa de las condiciones de primer orden y son fundamentales para la inferencia estadística en regresión lineal.
Implementemos estas fórmulas:
def calcular_estimadores_mc(x, y):
"""Calcula los estimadores de mínimos cuadrados"""
x_mean, y_mean = np.mean(x), np.mean(y)
beta1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean)**2)
beta0 = y_mean - beta1 * x_mean
return beta0, beta1
beta0_est, beta1_est = calcular_estimadores_mc(x, y)
print(f'Estimadores de mínimos cuadrados:')
print(f'β₀: {beta0_est:.4f} (verdadero: {beta0_true})')
print(f'β₁: {beta1_est:.4f} (verdadero: {beta1_true})')
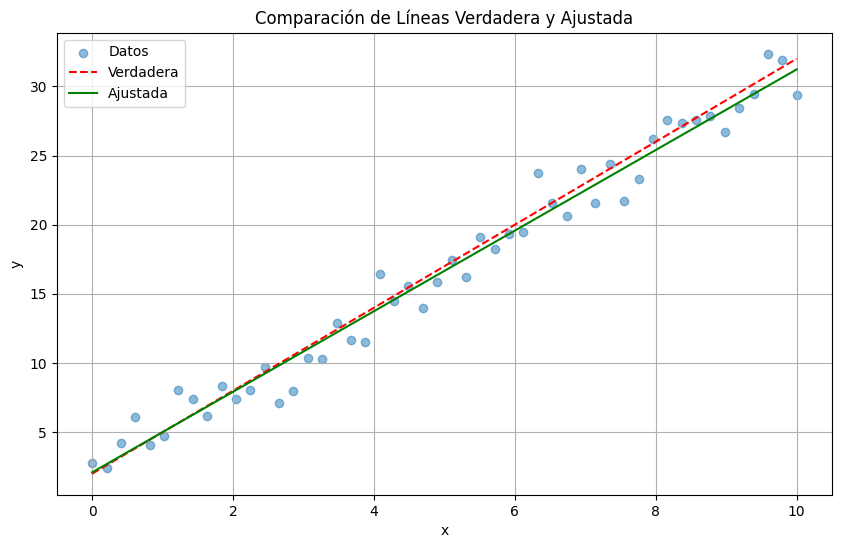
# Visualización del ajuste
plt.scatter(x, y, alpha=0.5, label='Datos')
plt.plot(x, beta0_true + beta1_true * x, 'r--', label='Verdadera')
plt.plot(x, beta0_est + beta1_est * x, 'g-', label='Ajustada')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Comparación de Líneas Verdadera y Ajustada')
plt.legend()
plt.grid(True)
plt.show()
Estimadores de mínimos cuadrados:
β₀: 2.0967 (verdadero: 2)
β₁: 2.9130 (verdadero: 3)
Observación
Los estimadores de mínimos cuadrados son insesgados y eficientes bajo los supuestos del modelo.
3. Propiedades de los Estimadores#
Propiedades Teóricas
Bajo los supuestos del modelo, los estimadores de mínimos cuadrados son:
Insesgados: \(E(\hat{\beta}_0) = \beta_0\) y \(E(\hat{\beta}_1) = \beta_1\)
De mínima varianza entre todos los estimadores lineales insesgados
Las varianzas de los estimadores son:
3.1 Insesgamiento#
3.1.1 Insesgamiento de \(\hat{\beta}_1\)#
Teorema
El estimador \(\hat{\beta}_1\) es insesgado, es decir, \(E(\hat{\beta}_1) = \beta_1\)
Demostración:
Dado que \(y_i = \beta_0 + \beta_1x_i + \epsilon_i\):
Sustituyendo:
3.1.2 Insesgamiento de \(\hat{\beta}_0\)#
Teorema
El estimador \(\hat{\beta}_0\) es insesgado, es decir, \(E(\hat{\beta}_0) = \beta_0\)
Demostración:
3.2 Varianzas de los Estimadores#
3.2.1 Varianza de \(\hat{\beta}_1\)#
Dado que \(var(y_i) = \sigma^2\) y los errores son independientes:
3.2.2 Varianza de \(\hat{\beta}_0\)#
Después de desarrollar los términos:
3.3 Teorema de Gauss-Markov#
Teorema de Gauss-Markov
Entre todos los estimadores lineales e insesgados de \(\beta_0\) y \(\beta_1\), los estimadores de mínimos cuadrados tienen varianza mínima.
3.3.1 Demostración del Teorema#
Sea \(\tilde{\beta}_1\) otro estimador lineal insesgado de \(\beta_1\):
Entonces:
3.4 Propiedades de los Residuos#
Los residuos \(\hat{\epsilon}_i = y_i - \hat{y}_i\) tienen las siguientes propiedades:
\(\sum_{i=1}^n \hat{\epsilon}_i = 0\)
\(\sum_{i=1}^n x_i\hat{\epsilon}_i = 0\)
\(\sum_{i=1}^n \hat{y}_i\hat{\epsilon}_i = 0\)
\(Cov(\hat{y}_i, \hat{\epsilon}_i) = 0\)
Note
Estas propiedades son fundamentales para la inferencia estadística y la validación del modelo.
3.5 Consecuencias Prácticas#
Eficiencia: Los estimadores MCO son los mejores estimadores lineales insesgados (BLUE).
Precisión:
La precisión de \(\hat{\beta}_1\) aumenta con:
Mayor variabilidad en x (\(\sum_{i=1}^n (x_i - \bar{x})^2\) grande)
Menor varianza del error (\(\sigma^2\) pequeño)
Mayor tamaño muestral (n)
Intervalo de Confianza:
Los intervalos de confianza serán más estrechos cuando:
Las varianzas sean menores
El tamaño muestral sea mayor
# Simulación para verificar insesgamiento
n_sims = 1000
beta0_sims = np.zeros(n_sims)
beta1_sims = np.zeros(n_sims)
for i in range(n_sims):
epsilon = np.random.normal(0, 1.5, n)
y_sim = beta0_true + beta1_true * x + epsilon
beta0_sims[i], beta1_sims[i] = calcular_estimadores_mc(x, y_sim)
print("Resultados de simulación:")
print(f'E(β₀): {np.mean(beta0_sims):.4f} (verdadero: {beta0_true})')
print(f'E(β₁): {np.mean(beta1_sims):.4f} (verdadero: {beta1_true})')
Resultados de simulación:
E(β₀): 2.0035 (verdadero: 2)
E(β₁): 2.9993 (verdadero: 3)
Observación
Los resultados de la simulación confirman que los estimadores de mínimos cuadrados son insesgados.
# Simulación para verificar varianzas
sigma2 = 1.5**2
var_beta0 = sigma2 * (1/n + np.mean(x)**2 / np.sum((x - np.mean(x))**2))
var_beta1 = sigma2 / np.sum((x - np.mean(x))**2)
print("Varianzas de los estimadores:")
print(f'var(β₀): {var_beta0:.4f}')
Varianzas de los estimadores:
var(β₀): 0.1747
4. Inferencia Estadística en Regresión Lineal#
4.1 Estimación de la Varianza (σ²)#
La varianza del error (σ²) es un parámetro crucial que mide la dispersión de los datos alrededor de la línea de regresión. Su estimación es fundamental para:
Calcular errores estándar de los coeficientes
Construir intervalos de confianza
Realizar pruebas de hipótesis
import numpy as np
from scipy import stats
def estimate_variance(y, y_pred, n_params=2):
"""
Estima la varianza del error en regresión lineal.
Parámetros:
-----------
y : array-like
Valores observados
y_pred : array-like
Valores predichos
n_params : int
Número de parámetros en el modelo (default=2 para regresión simple)
Retorna:
--------
float
Estimación de σ²
"""
n = len(y)
residuals = y - y_pred
sigma2 = np.sum(residuals**2) / (n - n_params)
return sigma2
# Ejemplo de uso
y_pred = beta0_est + beta1_est * x
sigma2_est = estimate_variance(y, y_pred)
print(f'σ² estimado: {sigma2_est:.4f}')
# Visualización de residuos
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.scatter(y_pred, y - y_pred, alpha=0.5)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Valores predichos')
plt.ylabel('Residuos')
plt.title('Gráfico de Residuos vs Valores Predichos')
plt.grid(True)
plt.show()
4.2 Pruebas de Hipótesis#
Las pruebas de hipótesis nos permiten evaluar la significancia estadística de los coeficientes.
def test_beta1(beta1, x, sigma2, alpha=0.05):
"""
Realiza prueba de hipótesis para β₁
H₀: β₁ = 0
H₁: β₁ ≠ 0
Parámetros:
-----------
beta1 : float
Estimación de β₁
x : array-like
Variable independiente
sigma2 : float
Varianza estimada
alpha : float
Nivel de significancia
Retorna:
--------
dict
Resultados del test
"""
n = len(x)
# Error estándar
se = np.sqrt(sigma2 / np.sum((x - np.mean(x))**2))
# Estadístico t
t_stat = beta1 / se
# Grados de libertad
df = n - 2
# Valor p
p_value = 2 * (1 - stats.t.cdf(abs(t_stat), df=df))
# Intervalo de confianza
t_crit = stats.t.ppf(1-alpha/2, df=df)
ci = (beta1 - t_crit * se, beta1 + t_crit * se)
return {
't_statistic': t_stat,
'p_value': p_value,
'confidence_interval': ci
}
# Ejemplo de uso
results = test_beta1(beta1_est, x, sigma2_est)
print(f"Estadístico t: {results['t_statistic']:.4f}")
print(f"Valor p: {results['p_value']:.4e}")
print(f"IC 95%: [{results['confidence_interval'][0]:.4f}, {results['confidence_interval'][1]:.4f}]")
4.3 Intervalos de Predicción#
Los intervalos de predicción proporcionan un rango para futuras observaciones.
def prediction_interval(x_new, x, beta0, beta1, sigma2, alpha=0.05):
"""
Calcula intervalo de predicción para nuevas observaciones
Parámetros:
-----------
x_new : float o array-like
Nuevos valores de x para predicción
x : array-like
Valores originales de x
beta0, beta1 : float
Coeficientes estimados
sigma2 : float
Varianza estimada
alpha : float
Nivel de significancia
Retorna:
--------
tuple
(predicción, límite inferior, límite superior)
"""
n = len(x)
x_mean = np.mean(x)
# Predicción puntual
y_pred = beta0 + beta1 * x_new
# Error estándar de predicción
se_pred = np.sqrt(sigma2 * (1 + 1/n +
(x_new - x_mean)**2 / np.sum((x - x_mean)**2)))
# Valor crítico
t_crit = stats.t.ppf(1-alpha/2, df=n-2)
# Intervalos
pi_lower = y_pred - t_crit * se_pred
pi_upper = y_pred + t_crit * se_pred
return y_pred, pi_lower, pi_upper
# Ejemplo de uso
x_new = np.linspace(min(x), max(x), 100)
predictions = prediction_interval(x_new, x, beta0_est, beta1_est, sigma2_est)
plt.figure(figsize=(10, 6))
plt.scatter(x, y, alpha=0.5, label='Datos observados')
plt.plot(x_new, predictions[0], 'r-', label='Regresión')
plt.fill_between(x_new, predictions[1], predictions[2],
alpha=0.2, label='Intervalo de predicción 95%')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Regresión con Intervalos de Predicción')
plt.legend()
plt.grid(True)
plt.show()
5. Bondad de Ajuste en Regresión Lineal#
5.1 Coeficiente de Determinación (R²)#
El R² es una medida fundamental que indica la proporción de la variabilidad en los datos que es explicada por el modelo de regresión.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
def calculate_r2(y, y_pred):
"""
Calcula el coeficiente de determinación R².
Parámetros:
-----------
y : array-like
Valores observados
y_pred : array-like
Valores predichos
Retorna:
--------
float
Valor de R²
dict
Componentes del cálculo (SST, SSR, SSE)
"""
# Suma total de cuadrados (SST)
ss_tot = np.sum((y - np.mean(y))**2)
# Suma de cuadrados de la regresión (SSR)
ss_reg = np.sum((y_pred - np.mean(y))**2)
# Suma de cuadrados del error (SSE)
ss_res = np.sum((y - y_pred)**2)
# Cálculo de R²
r2 = 1 - (ss_res / ss_tot)
# Alternativamente: r2 = ss_reg / ss_tot
return r2, {
'SST': ss_tot,
'SSR': ss_reg,
'SSE': ss_res
}
def plot_goodness_of_fit(y, y_pred, r2):
"""
Genera visualizaciones para evaluar la bondad de ajuste.
Parámetros:
-----------
y : array-like
Valores observados
y_pred : array-like
Valores predichos
r2 : float
Coeficiente de determinación
"""
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Gráfico de valores observados vs predichos
ax1.scatter(y, y_pred, alpha=0.5)
ax1.plot([min(y), max(y)], [min(y), max(y)], 'r--',
label='Línea de referencia')
ax1.set_xlabel('Valores Observados')
ax1.set_ylabel('Valores Predichos')
ax1.set_title(f'Observado vs Predicho (R² = {r2:.4f})')
ax1.grid(True)
ax1.legend()
# Gráfico Q-Q de residuos
residuals = y - y_pred
stats.probplot(residuals, dist="norm", plot=ax2)
ax2.set_title('Gráfico Q-Q de Residuos')
plt.tight_layout()
plt.show()
# Ejemplo de uso
r2, components = calculate_r2(y, y_pred)
plot_goodness_of_fit(y, y_pred, r2)
print("\nComponentes de la variabilidad:")
print(f"Variabilidad total (SST): {components['SST']:.4f}")
print(f"Variabilidad explicada (SSR): {components['SSR']:.4f}")
print(f"Variabilidad residual (SSE): {components['SSE']:.4f}")
print(f"\nR² = {r2:.4f}")
5.2 R² Ajustado#
El R² ajustado penaliza la adición de variables predictoras que no mejoran significativamente el modelo.
def adjusted_r2(r2, n, p):
"""
Calcula el R² ajustado.
Parámetros:
-----------
r2 : float
R² original
n : int
Número de observaciones
p : int
Número de predictores (sin incluir intercepto)
Retorna:
--------
float
R² ajustado
"""
adj_r2 = 1 - (1 - r2) * ((n - 1) / (n - p - 1))
return adj_r2
# Ejemplo de uso
n = len(y) # número de observaciones
p = 1 # número de predictores (sin intercepto)
adj_r2 = adjusted_r2(r2, n, p)
print(f"R² ajustado: {adj_r2:.4f}")
5.3 Medidas Adicionales de Ajuste#
def additional_metrics(y, y_pred):
"""
Calcula métricas adicionales de bondad de ajuste.
Parámetros:
-----------
y : array-like
Valores observados
y_pred : array-like
Valores predichos
Retorna:
--------
dict
Diccionario con diferentes métricas
"""
n = len(y)
residuals = y - y_pred
# Error cuadrático medio (MSE)
mse = np.mean(residuals**2)
# Raíz del error cuadrático medio (RMSE)
rmse = np.sqrt(mse)
# Error absoluto medio (MAE)
mae = np.mean(np.abs(residuals))
# Error porcentual absoluto medio (MAPE)
mape = np.mean(np.abs(residuals / y)) * 100
return {
'MSE': mse,
'RMSE': rmse,
'MAE': mae,
'MAPE': mape
}
# Ejemplo de uso
metrics = additional_metrics(y, y_pred)
for metric, value in metrics.items():
print(f"{metric}: {value:.4f}")
