Modelos Lineales: Fundamentos, Estimación y Evaluación#
Este cuaderno cubre de manera formal y aplicada los modelos de regresión lineal, desde su formulación matemática hasta su implementación en Python.
📌 Objetivos#
Definir y entender los modelos de regresión lineal.
Explicar los supuestos fundamentales del modelo.
Deducir matemáticamente la estimación de parámetros con mínimos cuadrados ordinarios (OLS).
Implementar los modelos en Python y evaluar su validez.
Aplicar pruebas estadísticas para validar los supuestos del modelo.
🚀 ¿Por qué son importantes los Modelos Lineales?#
Los modelos de regresión lineal son la base de numerosos métodos en estadística, econometría y machine learning. Se utilizan para:
Predicción de valores futuros.
Identificación de relaciones entre variables.
Evaluación de impacto en estudios experimentales.
Ahora, pasemos a su formulación matemática.
📊 Definición Matemática del Modelo Lineal#
Un modelo de regresión lineal múltiple con \(p\) variables predictoras se define como:
En notación matricial:
donde:
\(\mathbf{Y} \in \mathbb{R}^{n \times 1}\) es el vector de respuestas.
\(\mathbf{X} \in \mathbb{R}^{n \times (p+1)}\) es la matriz de diseño con una columna de unos para el intercepto.
\(\boldsymbol{\beta} \in \mathbb{R}^{(p+1) \times 1}\) es el vector de coeficientes.
\(\boldsymbol{\varepsilon} \in \mathbb{R}^{n \times 1}\) representa los errores aleatorios.
🔎 ¿Qué buscamos en el modelo?#
Estimaciones de los coeficientes \(\boldsymbol{\beta}\) que minimicen los errores.
Validación de los supuestos que garanticen la validez del modelo.
Pasemos a los supuestos fundamentales del modelo lineal.
📌 Estimación de Parámetros en Modelos Lineales#
La estimación de los parámetros de un modelo de regresión lineal múltiple se realiza mediante el método de mínimos cuadrados ordinarios (OLS, por sus siglas en inglés).
✅ Planteamiento del Problema#
Dado un conjunto de datos con \(n\) observaciones y \(p\) variables predictoras, podemos expresar el modelo en forma matricial como:
donde:
\(\mathbf{Y} \in \mathbb{R}^{n \times 1}\) es el vector de respuestas (variable dependiente).
\(\mathbf{X} \in \mathbb{R}^{n \times (p+1)}\) es la matriz de diseño, donde cada fila representa una observación y cada columna una variable predictora. Se incluye una columna de unos para representar el término intercepto.
\(\boldsymbol{\beta} \in \mathbb{R}^{(p+1) \times 1}\) es el vector de coeficientes a estimar.
\(\boldsymbol{\varepsilon} \in \mathbb{R}^{n \times 1}\) es el vector de errores aleatorios.
La matriz de diseño \(\mathbf{X}\) tiene la siguiente estructura:
donde la primera columna de unos representa el término intercepto \(\beta_0\).
🔍 Criterio de Estimación: Mínimos Cuadrados Ordinarios#
El objetivo del método de mínimos cuadrados ordinarios es encontrar los coeficientes \(\boldsymbol{\beta}\) que minimicen la suma de los cuadrados de los errores:
Para minimizar esta función, derivamos con respecto a \(\boldsymbol{\beta}\) y resolvemos:
Resolviendo para \(\boldsymbol{\beta}\):
Si la matriz \(\mathbf{X}^T \mathbf{X}\) es invertible, podemos despejar:
Esta es la solución de mínimos cuadrados ordinarios (OLS).
🧪 Propiedades de los Estimadores OLS#
Si los supuestos del modelo lineal se cumplen, los estimadores \(\hat{\boldsymbol{\beta}}\) presentan las siguientes propiedades:
Insesgadez:
\(\mathbb{E}[\hat{\boldsymbol{\beta}}] = \boldsymbol{\beta}\)
En promedio, los coeficientes estimados son iguales a los valores reales.
Varianza mínima (Eficiencia):
Entre todos los estimadores lineales insesgados, OLS tiene la menor varianza (propiedad de mínima varianza dentro de los estimadores lineales insesgados, BLUE).
Distribución Asintótica:
Si los errores son normales, los estimadores \(\hat{\boldsymbol{\beta}}\) siguen una distribución normal: $\( \hat{\boldsymbol{\beta}} \sim \mathcal{N}(\boldsymbol{\beta}, \sigma^2 (\mathbf{X}^T \mathbf{X})^{-1}) \)$
Si la muestra es grande, la distribución asintótica sigue siendo normal (por el Teorema del Límite Central).
🔬 Estimación de la Varianza del Error#
El error estándar de los coeficientes estimados se obtiene a partir de la varianza de los residuos:
donde:
\(\hat{\varepsilon}_i = Y_i - \hat{Y}_i\) son los residuos.
\(n - (p+1)\) es el número de grados de libertad, donde \(p+1\) representa los coeficientes estimados (incluyendo el intercepto).
La varianza de los coeficientes estimados se obtiene mediante:
📊 Implementación en Python#
A continuación, implementamos la estimación de parámetros usando numpy y statsmodels para validar la fórmula teórica.
import numpy as np
# Generamos datos simulados
np.random.seed(42)
X = np.random.rand(100, 2) * 10 # Dos predictores
Y = 3 + 2.5 * X[:, 0] + 1.8 * X[:, 1] + np.random.randn(100) * 2 # Relación lineal
# Agregamos una columna de unos para el intercepto
X_design = np.c_[np.ones(X.shape[0]), X]
# Estimación por mínimos cuadrados ordinarios (OLS)
beta_ols = np.linalg.inv(X_design.T @ X_design) @ X_design.T @ Y
# Mostramos los coeficientes estimados
print(f"Coeficientes estimados (OLS): {beta_ols}")
Coeficientes estimados (OLS): [2.54454453 2.56773335 1.87098921]
🛠️ Validación con statsmodels#
Para confirmar la estimación manual, utilizamos la biblioteca statsmodels.
import statsmodels.api as sm
# Ajustamos un modelo con statsmodels
X_sm = sm.add_constant(X) # Agregar intercepto
modelo = sm.OLS(Y, X_sm).fit()
# Mostramos los resultados
print(modelo.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.956
Model: OLS Adj. R-squared: 0.955
Method: Least Squares F-statistic: 1063.
Date: Thu, 03 Apr 2025 Prob (F-statistic): 1.09e-66
Time: 14:20:24 Log-Likelihood: -210.27
No. Observations: 100 AIC: 426.5
Df Residuals: 97 BIC: 434.4
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.5445 0.519 4.902 0.000 1.514 3.575
x1 2.5677 0.066 38.770 0.000 2.436 2.699
x2 1.8710 0.071 26.393 0.000 1.730 2.012
==============================================================================
Omnibus: 5.986 Durbin-Watson: 2.104
Prob(Omnibus): 0.050 Jarque-Bera (JB): 5.624
Skew: 0.439 Prob(JB): 0.0601
Kurtosis: 3.761 Cond. No. 19.5
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
📌 Implementación en Python#
Para verificar la estimación de los parámetros, utilizamos numpy para la solución manual y statsmodels para la validación.
import numpy as np
import pandas as pd
import statsmodels.api as sm
# Generamos datos simulados
np.random.seed(42)
X = np.random.rand(100, 2) * 10 # Dos predictores
Y = 3 + 2.5 * X[:, 0] + 1.8 * X[:, 1] + np.random.randn(100) * 2 # Relación lineal
# Agregamos una columna de unos para el intercepto
X_design = np.c_[np.ones(X.shape[0]), X]
# Estimación por mínimos cuadrados ordinarios (OLS)
beta_ols = np.linalg.inv(X_design.T @ X_design) @ X_design.T @ Y
# Mostramos los coeficientes estimados
print(f"Coeficientes estimados (OLS): {beta_ols}")
Coeficientes estimados (OLS): [2.54454453 2.56773335 1.87098921]
📌 Supuestos del Modelo Lineal#
Para que un modelo de regresión lineal sea válido, deben cumplirse los siguientes 5 supuestos fundamentales:
Linealidad: La relación entre las variables explicativas y la variable respuesta es lineal.
Independencia: Los errores \(\varepsilon_i\) son independientes.
Homoscedasticidad: La varianza de los errores es constante en todos los valores de \(X\).
Normalidad: Los errores siguen una distribución normal.
No Multicolinealidad: No hay correlación fuerte entre las variables explicativas.
Estos supuestos matemáticos garantizan la validez de las estimaciones y permiten realizar inferencias confiables. Estos supuestos son críticos para que los estimadores obtenidos mediante el método de mínimos cuadrados ordinarios (OLS) sean insesgados, eficientes y consistentes.
📌 Supuesto de Linealidad#
El supuesto de linealidad establece que la relación entre las variables independientes \(X\) y la variable dependiente \(Y\) debe ser lineal en los parámetros. Matemáticamente, el modelo de regresión lineal simple se expresa como:
donde:
\(Y_i\) es la variable dependiente.
\(X_i\) es la variable independiente.
\(\beta_0\) y \(\beta_1\) son los parámetros del modelo.
\(\varepsilon_i\) es el término de error, que recoge la variabilidad no explicada por \(X\).
Para el caso de regresión múltiple con \(p\) predictores:
El supuesto de linealidad no implica que los datos deban seguir una distribución lineal, sino que la relación funcional entre \(X\) y \(Y\) debe ser representable mediante una combinación lineal de los parámetros.
🔍 Evaluación del Supuesto de Linealidad#
Existen varios métodos para evaluar si la relación entre las variables es lineal:
Análisis gráfico: El gráfico de residuos vs. valores ajustados es una herramienta fundamental. Si los residuos presentan patrones sistemáticos (como curvaturas), la relación puede no ser lineal.
Prueba de Ramsey RESET: Una prueba formal que permite evaluar si el modelo omite términos no lineales significativos.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import reset_ramsey
sns.set(style="whitegrid")
📊 Análisis Gráfico: Residuos vs. Valores Ajustados#
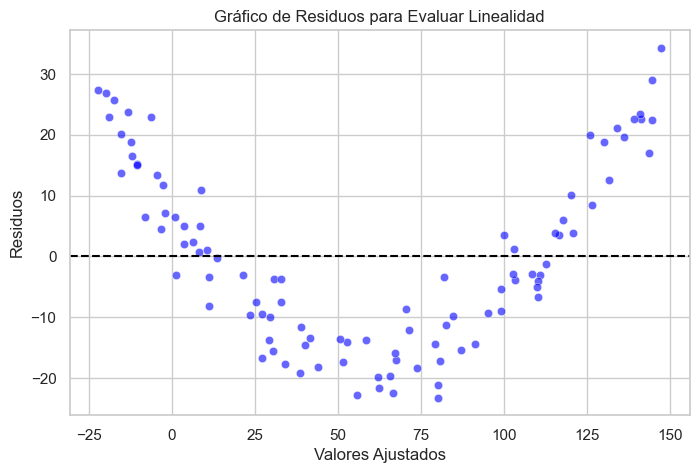
El análisis gráfico es una de las herramientas más intuitivas para evaluar la linealidad del modelo. Si el modelo es correctamente especificado, los residuos deben distribuirse aleatoriamente alrededor de cero sin presentar patrones.
🚨 Posibles señales de no linealidad en los residuos:#
Curvaturas: Indican que la relación entre \(X\) y \(Y\) puede ser cuadrática o polinómica.
Patrones sistemáticos: Sugieren la omisión de una transformación o variable explicativa.
A continuación, generamos un ejemplo con una relación cuadrática para visualizar cómo se comportan los residuos cuando la linealidad no se cumple.
# Generación de datos con una relación cuadrática
np.random.seed(42)
X = np.random.rand(100) * 10
Y_nolineal = 2.5 + 1.8 * X**2 + np.random.randn(100) * 5
# Ajuste de modelo lineal incorrecto
X_const = sm.add_constant(X)
modelo = sm.OLS(Y_nolineal, X_const).fit()
# Gráfico de residuos
plt.figure(figsize=(8, 5))
sns.scatterplot(x=modelo.fittedvalues, y=modelo.resid, color='blue', alpha=0.6)
plt.axhline(0, linestyle='dashed', color='black')
plt.xlabel("Valores Ajustados")
plt.ylabel("Residuos")
plt.title("Gráfico de Residuos para Evaluar Linealidad")
plt.show()
🧪 Prueba de Ramsey RESET#
La prueba de Ramsey RESET es un procedimiento estadístico que evalúa si el modelo de regresión omite términos no lineales importantes.
📌 ¿Qué evalúa esta prueba?#
La prueba consiste en incluir potencias de los valores ajustados en el modelo y evaluar si estas contribuyen significativamente a la explicación de la variable dependiente.
Matemáticamente, si nuestro modelo inicial es:
La prueba Ramsey RESET introduce términos adicionales:
donde \(\hat{Y}_i\) son los valores ajustados del modelo original. La hipótesis nula y alternativa son:
\(H_0\): El modelo está correctamente especificado (no se necesitan términos no lineales).
\(H_1\): El modelo está mal especificado (se requieren términos no lineales).
Si el p-valor es menor a 0.05, existe evidencia suficiente para rechazar \(H_0\) y concluir que el modelo no es lineal.
# Prueba de Ramsey RESET para especificación del modelo
reset_test = reset_ramsey(modelo)
print(f"Prueba de Ramsey RESET: estadístico = {reset_test.statistic:.3f}, p-valor = {reset_test.pvalue:.3f}")
if reset_test.pvalue < 0.05:
print("Se rechaza la hipótesis nula. Se recomienda incluir términos no lineales.")
else:
print("No hay evidencia suficiente para rechazar la hipótesis nula. La linealidad es adecuada.")
Prueba de Ramsey RESET: estadístico = 247.092, p-valor = 0.000
Se rechaza la hipótesis nula. Se recomienda incluir términos no lineales.
🔬 ¿Por qué funciona la prueba de Ramsey RESET?#
La prueba de Ramsey RESET (Regression Equation Specification Error Test) se basa en la idea de que si un modelo de regresión está correctamente especificado, entonces los valores ajustados \(\hat{Y}\) no deberían contener información adicional que explique \(Y\) más allá de lo que ya explican las variables independientes \(X\).
Matemáticamente, si nuestro modelo original es:
La prueba introduce términos no lineales de los valores ajustados \(\hat{Y}\) en el modelo de prueba:
donde \(\hat{Y}_i\) son los valores ajustados del modelo original.
Si el modelo original es correcto, los términos adicionales \(\gamma_1\) y \(\gamma_2\) deberían ser estadísticamente no significativos, ya que no deberían explicar variabilidad adicional en \(Y\).
📌 ¿Cómo se evalúa?#
Se realiza una prueba F para comparar el modelo original con el modelo extendido.
Se evalúa si agregar términos polinómicos mejora significativamente el ajuste del modelo.
📌 Interpretación:#
Si el p-valor es mayor a 0.05: No hay evidencia suficiente para rechazar la hipótesis nula, lo que sugiere que el modelo es adecuado.
Si el p-valor es menor a 0.05: Se rechaza la hipótesis nula, lo que indica que el modelo podría estar mal especificado y requerir términos no lineales.
A continuación, aplicamos la prueba de Ramsey RESET a nuestro modelo.
# Prueba de Ramsey RESET para especificación del modelo
reset_test = reset_ramsey(modelo)
print(f"Prueba de Ramsey RESET: estadístico = {reset_test.statistic:.3f}, p-valor = {reset_test.pvalue:.3f}")
if reset_test.pvalue < 0.05:
print("Se rechaza la hipótesis nula. Se recomienda incluir términos no lineales.")
else:
print("No hay evidencia suficiente para rechazar la hipótesis nula. La linealidad es adecuada.")
Prueba de Ramsey RESET: estadístico = 247.092, p-valor = 0.000
Se rechaza la hipótesis nula. Se recomienda incluir términos no lineales.
📌 Supuesto de Independencia de los Errores#
El supuesto de independencia establece que los errores \(\varepsilon_i\) de un modelo de regresión deben ser mutuamente independientes. En otras palabras, el valor del error en una observación no debe estar correlacionado con el valor del error en otra observación.
Matemáticamente, esto se expresa como:
donde \(\text{Cov}\) representa la covarianza entre los errores. Si esta covarianza es distinta de cero, hay dependencia en los errores, lo que puede indicar la presencia de autocorrelación.
✅ Importancia del Supuesto#
El incumplimiento del supuesto de independencia puede llevar a:
Inferencias erróneas: Si los errores están correlacionados, las pruebas de hipótesis y los intervalos de confianza pueden ser incorrectos.
Coeficientes ineficientes: Aunque los estimadores de Mínimos Cuadrados Ordinarios (OLS) siguen siendo insesgados, dejan de ser eficientes y pueden tener varianzas más altas de lo esperado.
Predicciones sesgadas: Un modelo con errores correlacionados puede generar predicciones incorrectas, especialmente en datos secuenciales o temporales.
🔍 Métodos de Detección#
Para evaluar si los errores son independientes, utilizamos las siguientes herramientas:
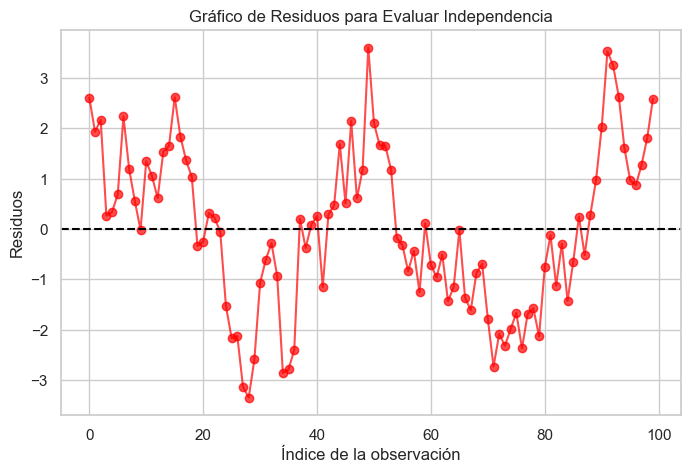
Análisis gráfico: El gráfico de residuos en función del tiempo o del índice permite identificar patrones en los residuos.
Prueba de Durbin-Watson: Es una prueba estadística diseñada para detectar autocorrelación de primer orden en los errores.
# Generación de datos con autocorrelación en los errores
np.random.seed(42)
X_dep = np.random.rand(100) * 10
Y_dependencia = 2.5 + 1.8 * X_dep + np.cumsum(np.random.randn(100)) # Ruido acumulado genera dependencia
# Ajuste del modelo
X_dep_const = sm.add_constant(X_dep)
modelo_dep = sm.OLS(Y_dependencia, X_dep_const).fit()
# Gráfico de residuos en función del índice
plt.figure(figsize=(8, 5))
plt.plot(modelo_dep.resid, marker='o', linestyle='-', color='red', alpha=0.7)
plt.axhline(0, linestyle='dashed', color='black')
plt.xlabel("Índice de la observación")
plt.ylabel("Residuos")
plt.title("Gráfico de Residuos para Evaluar Independencia")
plt.show()
🧪 Prueba de Durbin-Watson#
La prueba de Durbin-Watson evalúa la presencia de autocorrelación de primer orden en los errores del modelo.
📌 ¿Qué evalúa esta prueba?#
La autocorrelación de primer orden se define como:
Donde \(\rho\) representa el grado de correlación entre los errores consecutivos.
La estadística de Durbin-Watson (\(DW\)) se calcula como:
📌 Interpretación:#
\(DW \approx 2\): No hay autocorrelación en los errores (modelo adecuado).
\(DW < 1.5\): Hay autocorrelación positiva (los errores consecutivos tienden a ser similares).
\(DW > 2.5\): Hay autocorrelación negativa (los errores consecutivos tienden a alternar signos).
A continuación, aplicamos la prueba de Durbin-Watson a nuestro modelo.
from statsmodels.stats.stattools import durbin_watson
# Prueba de Durbin-Watson para independencia de los errores
dw_stat_dep = durbin_watson(modelo_dep.resid)
print(f"Estadístico Durbin-Watson: {dw_stat_dep:.3f} (Cerca de 2 indica independencia)")
if dw_stat_dep < 1.5:
print("Posible autocorrelación positiva en los errores.")
elif dw_stat_dep > 2.5:
print("Posible autocorrelación negativa en los errores.")
else:
print("No hay evidencia de autocorrelación en los errores.")
Estadístico Durbin-Watson: 0.330 (Cerca de 2 indica independencia)
Posible autocorrelación positiva en los errores.
🔧 Métodos para Corregir la Autocorrelación#
Si se detecta autocorrelación en los errores, existen diversas estrategias para corregir el problema:
Modelos de series temporales:
Si los datos presentan una estructura temporal, utilizar modelos como ARIMA o regresión con términos autorregresivos.
Incluir variables omitidas:
A veces, la autocorrelación se debe a la omisión de una variable explicativa clave que no ha sido incluida en el modelo.
Regresión con Errores Estructurados:
Aplicar modelos con errores heterocedásticos y autorregresivos (HAC) mediante técnicas como la corrección de Newey-West.
📌 Supuesto de Homocedasticidad#
El supuesto de homocedasticidad establece que la varianza de los errores \(\varepsilon_i\) es constante en todos los niveles de las variables explicativas. Matemáticamente, se expresa como:
Si este supuesto no se cumple y la varianza de los errores varía con los valores de \(X\), se dice que el modelo presenta heterocedasticidad.
✅ Importancia del Supuesto#
La homocedasticidad es fundamental para que los intervalos de confianza y pruebas de hipótesis sean correctos. Si hay heterocedasticidad:
Los estimadores de mínimos cuadrados ordinarios (OLS) siguen siendo insesgados, pero pierden eficiencia, lo que afecta la precisión de las predicciones.
Las pruebas estadísticas pueden arrojar resultados incorrectos porque los errores estándar de los coeficientes pueden estar mal estimados.
El modelo puede dar más peso a ciertas observaciones, afectando la interpretación de los coeficientes.
🔍 Métodos de Detección#
Para evaluar si los errores son homocedásticos, utilizamos las siguientes herramientas:
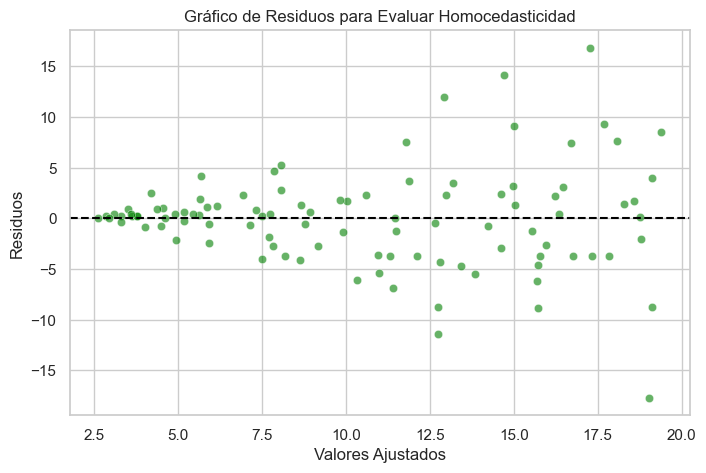
Gráfico de residuos vs. valores ajustados: Si la dispersión de los residuos cambia a medida que aumentan los valores ajustados, hay indicios de heterocedasticidad.
Prueba de Breusch-Pagan: Evalúa si la varianza de los errores depende de los valores de las variables explicativas.
# Generación de datos con heterocedasticidad
np.random.seed(42)
X_hetero = np.random.rand(100) * 10
Y_hetero = 2.5 + 1.8 * X_hetero + (X_hetero * np.random.randn(100)) # Errores aumentan con X
# Ajuste del modelo
X_hetero_const = sm.add_constant(X_hetero)
modelo_hetero = sm.OLS(Y_hetero, X_hetero_const).fit()
# Gráfico de residuos
plt.figure(figsize=(8, 5))
sns.scatterplot(x=modelo_hetero.fittedvalues, y=modelo_hetero.resid, color='green', alpha=0.6)
plt.axhline(0, linestyle='dashed', color='black')
plt.xlabel("Valores Ajustados")
plt.ylabel("Residuos")
plt.title("Gráfico de Residuos para Evaluar Homocedasticidad")
plt.show()
🧪 Prueba de Breusch-Pagan#
La prueba de Breusch-Pagan evalúa si la varianza de los errores está relacionada con los valores de las variables explicativas.
📌 ¿Qué evalúa esta prueba?#
Si la varianza de los errores depende de \(X\), entonces existe heterocedasticidad. La prueba se basa en la siguiente regresión auxiliar:
Se realiza una prueba de chi-cuadrado para determinar si los coeficientes \(\alpha_i\) son significativamente diferentes de cero.
📌 Hipótesis de la prueba:#
\(H_0\): La varianza de los errores es constante (homocedasticidad).
\(H_1\): La varianza de los errores depende de \(X\) (heterocedasticidad).
Si el p-valor es menor a 0.05, se rechaza la hipótesis nula y se concluye que el modelo presenta heterocedasticidad.
from statsmodels.stats.diagnostic import het_breuschpagan
# Prueba de Breusch-Pagan para homocedasticidad
_, pval_bp, _, _ = het_breuschpagan(modelo_hetero.resid, X_hetero_const)
print(f"Prueba de Breusch-Pagan: p-valor = {pval_bp:.3f} (p > 0.05 indica varianza constante)")
if pval_bp < 0.05:
print("Se detecta heterocedasticidad en el modelo.")
else:
print("No hay evidencia suficiente de heterocedasticidad.")
Prueba de Breusch-Pagan: p-valor = 0.000 (p > 0.05 indica varianza constante)
Se detecta heterocedasticidad en el modelo.
🔧 Métodos para Corregir la Heterocedasticidad#
Si la heterocedasticidad es detectada en el modelo, se pueden emplear diversas estrategias para corregirla:
Transformaciones de la variable dependiente:
Aplicar logaritmos o raíces cuadradas a la variable \(Y\) puede estabilizar la varianza.
Regresión ponderada:
Dar más peso a las observaciones con menor varianza y menos peso a las observaciones con mayor varianza.
Modelos de estimación robusta:
Usar errores estándar robustos de White para ajustar las pruebas de hipótesis y obtener estimaciones correctas.
Modelos de regresión generalizada:
En modelos más avanzados, se pueden utilizar modelos como GLS (Generalized Least Squares) para corregir heterocedasticidad explícitamente.
📌 Supuesto de Normalidad de los Errores#
El supuesto de normalidad de los errores establece que los residuos del modelo de regresión deben seguir una distribución normal con media cero y varianza constante. Matemáticamente:
donde \(\mathcal{N}(0, \sigma^2)\) denota una distribución normal con media \(0\) y varianza \(\sigma^2\).
Este supuesto es fundamental para realizar pruebas de hipótesis válidas sobre los coeficientes del modelo.
✅ Importancia del Supuesto#
Inferencias precisas: La normalidad de los errores garantiza que las pruebas estadísticas sobre los coeficientes sean válidas.
Correcta construcción de intervalos de confianza: Si los errores no son normales, los intervalos de confianza y los valores p pueden estar mal estimados.
Modelos con supuestos fuertes: Algunos métodos avanzados, como la regresión Bayesiana, requieren supuestos más estrictos sobre la distribución de los errores.
Si el tamaño muestral es grande, el Teorema del Límite Central permite que las estimaciones sean válidas aún si los errores no son perfectamente normales.
🔍 Métodos de Detección#
Para evaluar si los errores siguen una distribución normal, utilizamos las siguientes herramientas:
Histograma y Gráfico de Densidad: Nos permite inspeccionar visualmente si los residuos tienen forma de campana.
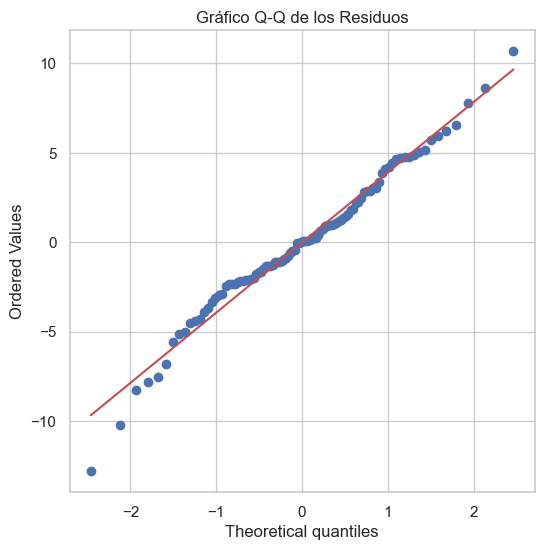
Gráfico Q-Q (Quantile-Quantile): Compara la distribución empírica de los errores con una distribución normal teórica.
Prueba de Shapiro-Wilk: Una prueba estadística para verificar si los errores siguen una distribución normal.
# Generación de datos con errores no normales
np.random.seed(42)
X_nonnormal = np.random.rand(100) * 10
Y_nonnormal = 2.5 + 1.8 * X_nonnormal + np.random.laplace(0, 3, 100) # Errores con distribución Laplace
# Ajuste del modelo
X_nonnormal_const = sm.add_constant(X_nonnormal)
modelo_nonnormal = sm.OLS(Y_nonnormal, X_nonnormal_const).fit()
# Histograma de los residuos
plt.figure(figsize=(8, 5))
sns.histplot(modelo_nonnormal.resid, kde=True, color='purple', bins=15)
plt.xlabel("Residuos")
plt.title("Distribución de los Residuos (Evaluación de Normalidad)")
plt.show()

📊 Gráfico Q-Q (Quantile-Quantile)#
El gráfico Q-Q compara los cuantiles de los residuos con los cuantiles de una distribución normal teórica. Si los residuos siguen una distribución normal, los puntos deben estar alineados sobre la diagonal.
# Gráfico Q-Q para evaluar normalidad
import scipy.stats as stats
plt.figure(figsize=(6, 6))
stats.probplot(modelo_nonnormal.resid, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de los Residuos")
plt.show()
🧪 Prueba de Shapiro-Wilk#
La prueba de Shapiro-Wilk evalúa la hipótesis de que los residuos siguen una distribución normal.
📌 ¿Qué evalúa esta prueba?#
Se calcula el coeficiente \(W\) que mide la correlación entre los valores observados y los valores esperados de una distribución normal.
📌 Hipótesis de la prueba:#
\(H_0\): Los errores siguen una distribución normal.
\(H_1\): Los errores no siguen una distribución normal.
Si el p-valor es menor a 0.05, se rechaza la hipótesis nula y se concluye que los errores no siguen una distribución normal.
from scipy.stats import shapiro
# Prueba de Shapiro-Wilk para normalidad
shapiro_stat, shapiro_pval = shapiro(modelo_nonnormal.resid)
print(f"Prueba de Shapiro-Wilk: p-valor = {shapiro_pval:.3f} (p > 0.05 indica normalidad)")
if shapiro_pval < 0.05:
print("Se detecta no normalidad en los errores.")
else:
print("No hay evidencia suficiente para rechazar la normalidad.")
Prueba de Shapiro-Wilk: p-valor = 0.250 (p > 0.05 indica normalidad)
No hay evidencia suficiente para rechazar la normalidad.
🔧 Métodos para Corregir la No Normalidad#
Si se detecta que los errores no son normales, existen diversas estrategias para mitigar el problema:
Transformaciones de la variable dependiente:
Aplicar logaritmos, raíz cuadrada o transformaciones de Box-Cox para modificar la distribución de los residuos.
Uso de estimadores robustos:
Aplicar métodos como regresión robusta (Huber, RANSAC) que no dependen fuertemente de la normalidad de los errores.
Aumento del tamaño de la muestra:
Si el tamaño muestral es pequeño, la normalidad de los errores puede no observarse. Al aumentar la muestra, el Teorema del Límite Central asegura que las inferencias sigan siendo válidas.
Usar modelos alternativos:
Si los residuos siguen una distribución específica distinta de la normal, considerar modelos como regresión cuantílica o modelos de distribución flexible.
📌 Supuesto de No Multicolinealidad#
El supuesto de no multicolinealidad establece que las variables explicativas en un modelo de regresión no deben estar altamente correlacionadas entre sí. Si existe una fuerte relación lineal entre dos o más predictores, se produce multicolinealidad, lo que dificulta la estimación precisa de los coeficientes.
Matemáticamente, si una variable explicativa \(X_j\) puede expresarse aproximadamente como una combinación lineal de otras variables:
entonces existe colinealidad.
✅ Importancia del Supuesto#
Si las variables predictoras están altamente correlacionadas:
Los coeficientes de regresión se vuelven inestables: Pequeñas variaciones en los datos pueden causar grandes cambios en las estimaciones de los coeficientes.
Dificultad en la interpretación: Es difícil determinar el impacto individual de cada variable en la variable dependiente.
Aumento de la varianza de los coeficientes estimados: Lo que reduce la precisión del modelo.
🔍 Métodos de Detección#
Para evaluar si el modelo presenta multicolinealidad, utilizamos:
Matriz de correlación: Si dos variables tienen una correlación mayor a 0.8 o 0.9, hay riesgo de multicolinealidad.
Factor de Inflación de la Varianza (VIF): Un VIF mayor a 10 indica una correlación muy alta entre variables predictoras.
from statsmodels.stats.outliers_influence import variance_inflation_factor
# Generar datos con alta correlación
np.random.seed(42)
X1 = np.random.rand(100) * 10
X2 = X1 + np.random.randn(100) * 0.1 # Segunda variable altamente correlacionada con X1
X3 = np.random.rand(100) * 10 # Variable independiente
# Crear DataFrame
df_multicolinealidad = pd.DataFrame({"X1": X1, "X2": X2, "X3": X3})
# Calcular la matriz de correlación
correlation_matrix = df_multicolinealidad.corr()
print("Matriz de correlación:")
print(correlation_matrix)
# Calcular el VIF para cada variable
vif_data = pd.DataFrame()
vif_data["Variable"] = df_multicolinealidad.columns
vif_data["VIF"] = [variance_inflation_factor(df_multicolinealidad.values, i) for i in range(df_multicolinealidad.shape[1])]
print("Factor de Inflación de la Varianza (VIF):")
print(vif_data)
Matriz de correlación:
X1 X2 X3
X1 1.000000 0.999536 -0.028591
X2 0.999536 1.000000 -0.025931
X3 -0.028591 -0.025931 1.000000
Factor de Inflación de la Varianza (VIF):
Variable VIF
0 X1 3824.560895
1 X2 3843.946662
2 X3 2.238342
🧪 Interpretación del Factor de Inflación de la Varianza (VIF)#
El VIF mide cuánto aumenta la varianza de un coeficiente debido a la correlación con otras variables.
📌 Interpretación:#
VIF \(\approx 1\): No hay multicolinealidad.
VIF entre 5 y 10: Multicolinealidad moderada (posible problema).
VIF > 10: Multicolinealidad severa (problema grave).
Si el VIF es alto, significa que la variable está fuertemente correlacionada con otras variables y puede afectar la estabilidad del modelo.
🔧 Métodos para Corregir la Multicolinealidad#
Si se detecta multicolinealidad en el modelo, existen varias estrategias para corregir el problema:
Eliminar una de las variables correlacionadas:
Si dos variables tienen una correlación superior a 0.9, considerar eliminar una de ellas.
Usar técnicas de reducción de dimensionalidad:
Aplicar Análisis de Componentes Principales (PCA) para reducir la redundancia en los datos.
Transformaciones matemáticas:
Si las variables representan información similar, considerar su combinación en una única variable sintética.
Usar regularización (Ridge Regression o Lasso):
Estos métodos penalizan coeficientes grandes y reducen el impacto de la multicolinealidad.
📌 Diagnóstico Automático de Supuestos en Modelos Lineales#
Este cuaderno proporciona una función en Python que evalúa automáticamente los 5 supuestos fundamentales del modelo de regresión lineal:
✅ Supuesto de Linealidad: Gráfico de residuos vs. valores ajustados y prueba de Ramsey RESET.
✅ Supuesto de Independencia: Prueba de Durbin-Watson para detectar autocorrelación en los errores.
✅ Supuesto de Homocedasticidad: Prueba de Breusch-Pagan para detectar cambios en la varianza de los errores.
✅ Supuesto de Normalidad: Histograma de residuos, gráfico Q-Q y prueba de Shapiro-Wilk.
✅ Supuesto de No Multicolinealidad: Matriz de correlación y Factor de Inflación de la Varianza (VIF).
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan
from statsmodels.stats.stattools import durbin_watson
from statsmodels.stats.outliers_influence import reset_ramsey, variance_inflation_factor
from scipy.stats import shapiro
from scipy import stats
sns.set(style="whitegrid")
def diagnostico_modelo(modelo, X, Y):
"""
Evalúa los cinco supuestos del modelo de regresión lineal.
Parámetros:
modelo : statsmodels.regression.linear_model.RegressionResultsWrapper
Modelo ajustado con statsmodels OLS.
X : ndarray o DataFrame
Matriz de predictores (sin la columna de unos para el intercepto).
Y : ndarray o Series
Vector de valores observados de la variable dependiente.
"""
residuos = modelo.resid
valores_ajustados = modelo.fittedvalues
print("🔍 Evaluación de Supuestos del Modelo Lineal")
# 1. Supuesto de Linealidad
plt.figure(figsize=(8, 5))
sns.scatterplot(x=valores_ajustados, y=residuos, color='blue', alpha=0.6)
plt.axhline(0, linestyle='dashed', color='black')
plt.xlabel("Valores Ajustados")
plt.ylabel("Residuos")
plt.title("Gráfico de Residuos vs. Valores Ajustados (Evaluación de Linealidad)")
plt.show()
# Prueba de Ramsey RESET
reset_test = reset_ramsey(modelo)
print(f"📌 Prueba de Ramsey RESET: estadístico = {reset_test.statistic:.3f}, p-valor = {reset_test.pvalue:.3f}")
if reset_test.pvalue < 0.05:
print("❌ Se recomienda incluir términos no lineales en el modelo.")
else:
print("✅ No hay evidencia de no linealidad en el modelo.")
# 2. Supuesto de Independencia
dw_stat = durbin_watson(residuos)
print(f"📌 Prueba de Durbin-Watson: {dw_stat:.3f} (Cerca de 2 indica independencia)")
if dw_stat < 1.5:
print("❌ Posible autocorrelación positiva en los errores.")
elif dw_stat > 2.5:
print("❌ Posible autocorrelación negativa en los errores.")
else:
print("✅ No hay evidencia de autocorrelación en los errores.")
# 3. Supuesto de Homocedasticidad
_, pval_bp, _, _ = het_breuschpagan(residuos, modelo.model.exog)
print(f"📌 Prueba de Breusch-Pagan: p-valor = {pval_bp:.3f} (p > 0.05 indica varianza constante)")
if pval_bp < 0.05:
print("❌ Se detecta heterocedasticidad en el modelo.")
else:
print("✅ No hay evidencia suficiente de heterocedasticidad.")
# 4. Supuesto de Normalidad
plt.figure(figsize=(8, 5))
sns.histplot(residuos, kde=True, color='purple', bins=15)
plt.xlabel("Residuos")
plt.title("Distribución de los Residuos (Evaluación de Normalidad)")
plt.show()
plt.figure(figsize=(6, 6))
stats.probplot(residuos, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de los Residuos")
plt.show()
shapiro_stat, shapiro_pval = shapiro(residuos)
print(f"📌 Prueba de Shapiro-Wilk: p-valor = {shapiro_pval:.3f} (p > 0.05 indica normalidad)")
if shapiro_pval < 0.05:
print("❌ Se detecta no normalidad en los errores.")
else:
print("✅ No hay evidencia suficiente para rechazar la normalidad.")
# 5. Supuesto de No Multicolinealidad
vif_data = pd.DataFrame()
vif_data["Variable"] = [f"X{i}" for i in range(1, X.shape[1] + 1)]
vif_data["VIF"] = [variance_inflation_factor(X, i) for i in range(X.shape[1])]
print("📌 Factor de Inflación de la Varianza (VIF):")
print(vif_data)
if vif_data["VIF"].max() > 10:
print("❌ Se detecta un problema de multicolinealidad en el modelo.")
print("✅ Diagnóstico Completo")
📊 Aplicación de la Función#
Probemos la función de diagnóstico en un modelo de regresión ajustado con statsmodels.
# Generación de datos simulados
np.random.seed(42)
X_test = np.random.rand(100, 2) * 10 # Dos predictores
Y_test = 3 + 2.5 * X_test[:, 0] + 1.8 * X_test[:, 1] + np.random.randn(100) * 2 # Relación lineal
# Ajustamos un modelo con statsmodels
X_sm_test = sm.add_constant(X_test) # Agregar intercepto
modelo_test = sm.OLS(Y_test, X_sm_test).fit()
# Ejecutamos el diagnóstico automático
diagnostico_modelo(modelo_test, X_test, Y_test)
🔍 Evaluación de Supuestos del Modelo Lineal
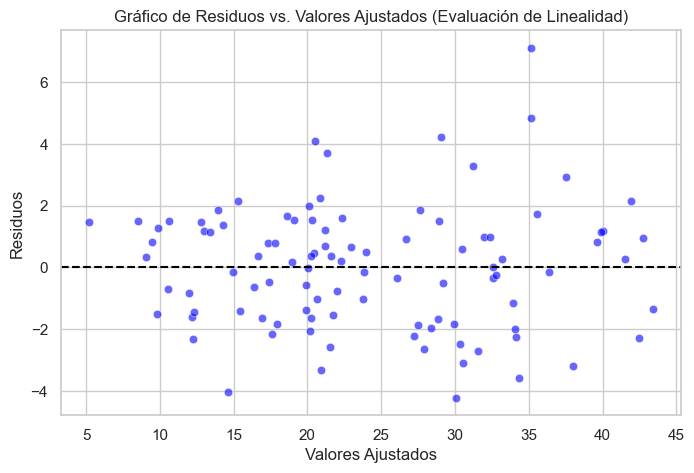
📌 Prueba de Ramsey RESET: estadístico = 1.155, p-valor = 0.336
✅ No hay evidencia de no linealidad en el modelo.
📌 Prueba de Durbin-Watson: 2.104 (Cerca de 2 indica independencia)
✅ No hay evidencia de autocorrelación en los errores.
📌 Prueba de Breusch-Pagan: p-valor = 0.031 (p > 0.05 indica varianza constante)
❌ Se detecta heterocedasticidad en el modelo.
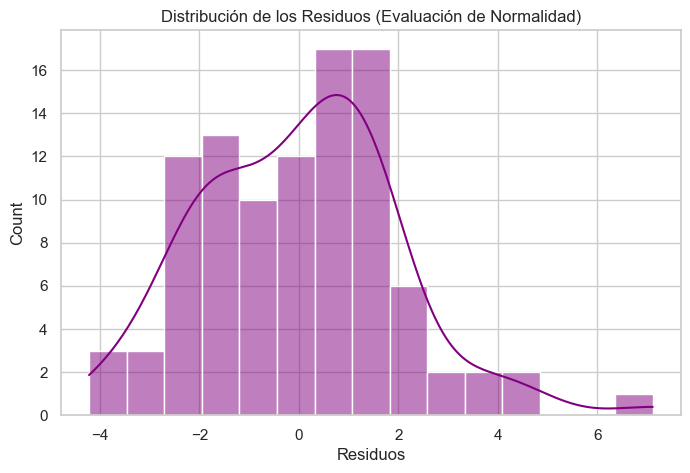
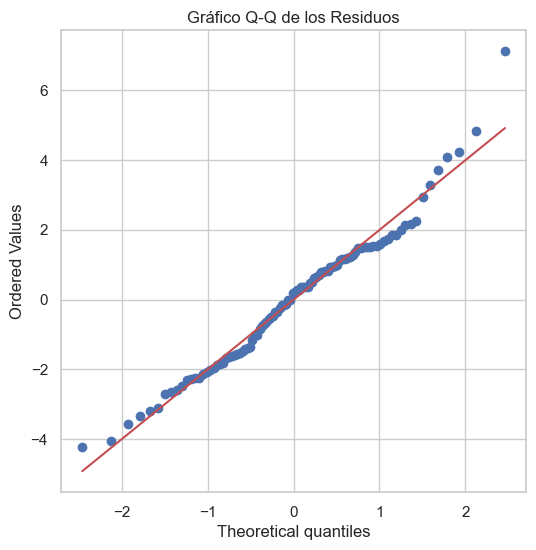
📌 Prueba de Shapiro-Wilk: p-valor = 0.070 (p > 0.05 indica normalidad)
✅ No hay evidencia suficiente para rechazar la normalidad.
📌 Factor de Inflación de la Varianza (VIF):
Variable VIF
0 X1 2.077077
1 X2 2.077077
✅ Diagnóstico Completo
